1911. Четырёхугольник ABCD
, диагонали которого взаимно перпендикулярны, вписан в окружность с центром O
. Найдите расстояние от точки O
до стороны AB
, если известно, что CD=a
.
Ответ. \frac{1}{2}a
.
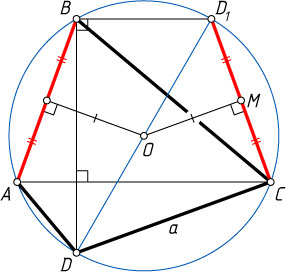
Указание. Проведите диаметр DD_{1}
.
Решение. Первый способ. Проведём диаметр DD_{1}
. Тогда \angle DBD_{1}=90^{\circ}
, поэтому BD_{1}\parallel AC
, значит, CD_{1}=AB
. Перпендикуляр, опущенный из центра O
на хорду CD_{1}
, проходит через середину M
этой хорды, поэтому OM
— средняя линия треугольника DD_{1}C
, OM=\frac{1}{2}CD=\frac{1}{2}a
. Поскольку равные хорды равноудалены от центра окружности, то расстояние от центра окружности до хорды AB
также равно \frac{1}{2}a
.
Второй способ. Опустим перпендикуляр OM
из центра окружности на сторону CD
. Обозначим \angle DOM=\alpha
, \angle ACB=\beta
. Тогда (см. задачу 25)
90^{\circ}=\frac{\smile CD+\smile AB}{2}=\frac{2\alpha+2\beta}{2}=\alpha+\beta.
Пусть радиус окружности равен R
. Тогда
OM=OD\cos\angle DOM=R\cos\alpha=R\cos(90^{\circ}-\beta)=R\sin\beta=
=\frac{1}{2}\cdot2R\sin\beta=\frac{1}{2}AB.
Что и требовалось доказать.
Примечание. Верно и обратное: если во вписанном четырёхугольнике ABCD
расстояние от центра O
окружности до стороны CD
вдвое меньше стороны AB
, то диагонали четырёхугольника перпендикулярны.
Доказательство. Опустим перпендикуляр OM
из центра окружности на сторону CD
. Обозначим \angle DOM=\alpha
, \angle ACB=\beta
. Тогда
OM=OD\cos\angle DOM=R\cos\alpha,
а так как по теореме синусов
2R\sin\beta=AB=2OM=2\cdot R\cos\alpha,
то \sin\alpha=\sin\beta
. Тогда угол между диагоналями четырёхугольника равен
\frac{\smile CD+\smile AB}{2}=\frac{2\alpha+2\beta}{2}=\alpha+\beta=90^{\circ}.
Что и требовалось доказать.
