1923. Диагонали трапеции взаимно перпендикулярны, а средняя линия равна 5. Найдите отрезок, соединяющий середины оснований.
Ответ. 5.
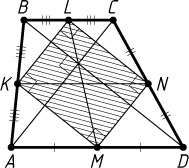
Указание. Четырёхугольник с вершинами в серединах сторон данной трапеции — прямоугольник (см. задачу 1204).
Решение. Пусть L
и M
— середины оснований соответственно BC
и AD
трапеции ABCD
, а K
и N
— середины боковых сторон AB
и CD
соответственно. Тогда KL
и MN
— средние линии треугольников ABC
и ADC
с общей стороной AC
, поэтому KL=MN
и KL\parallel MN
, значит, четырёхугольник KLNM
— параллелограмм. Его стороны KL
и LN
соответственно параллельны взаимно перпендикулярным диагоналям AC
и BD
трапеции ABCD
, значит, KLNM
— прямоугольник. Диагонали прямоугольника равны, следовательно, LM=KN=5
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.13, с. 24
