1947. Дан треугольник со сторонами a
, b
и c
. Докажите, что если медианы, проведённые к сторонам a
и b
, взаимно перпендикулярны, то a^{2}+b^{2}=5c^{2}
.
Указание. Медианы треугольника делятся точкой пересечения в отношении 2:1
, считая от вершины.
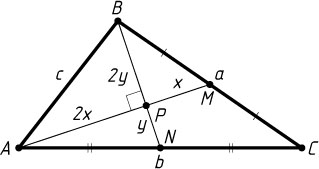
Решение. Пусть медианы AM
и BN
треугольника ABC
со сторонами AB=c
, AC=b
и BC=a
взаимно перпендикулярны и пересекаются в точке P
. Обозначим PM=x
, PN=y
. Тогда по теореме медианах AP=2x
, BP=2y
. Применив теорему Пифагора к прямоугольным треугольникам APN
и BPM
, получим, что
4x^{2}+y^{2}=\frac{b^{2}}{4},~x^{2}+4y^{2}=\frac{a^{2}}{4}.
Поэтому
5x^{2}+5y^{2}=\frac{a^{2}+b^{2}}{4},~x^{2}+y^{2}=\frac{a^{2}+b^{2}}{20}.
Из прямоугольного треугольника APB
, находим, что
c^{2}=AB^{2}=4x^{2}+4y^{2}=\frac{a^{2}+b^{2}}{5},
откуда a^{2}+b^{2}=5c^{2}
.
Второй способ. Пусть AM
, BN
и CK
— медианы треугольника ABC
со сторонами AB=c
, AC=b
и BC=a
. Обозначим
\overrightarrow{AB}=\overrightarrow{c},~\overrightarrow{BC}=\overrightarrow{a},~\overrightarrow{CA}=\overrightarrow{b}.
Тогда
|\overrightarrow{c}|=c,~|\overrightarrow{a}|=a,~|\overrightarrow{b}|=b,
\overrightarrow{AM}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})=\frac{1}{2}(\overrightarrow{c}-\overrightarrow{b}),
\overrightarrow{BN}=\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{BA})=\frac{1}{2}(\overrightarrow{a}-\overrightarrow{c}),
\overrightarrow{CK}=\frac{1}{2}(\overrightarrow{CA}+\overrightarrow{CB})=\frac{1}{2}(\overrightarrow{b}-\overrightarrow{c}),
Поскольку AM\perp BN
, то скалярное произведение векторов \overrightarrow{AM}
и \overrightarrow{BN}
равно 0, т. е. \overrightarrow{AM}\cdot\overrightarrow{BN}=0
. Следовательно,
\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})\cdot\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{BA})=0~\Rightarrow~(\overrightarrow{c}-\overrightarrow{b})(\overrightarrow{a}-\overrightarrow{c})=0~\Rightarrow
\Rightarrow~\overrightarrow{a}\cdot\overrightarrow{c}-\overrightarrow{a}\cdot\overrightarrow{b}-c^{2}+\overrightarrow{b}\overrightarrow{c}=0~\Rightarrow~\overrightarrow{c}(\overrightarrow{a}+\overrightarrow{b})-c^{2}-\overrightarrow{a}\cdot\overrightarrow{b}=0~\Rightarrow
\Rightarrow~-c^{2}-c^{2}-\overrightarrow{a}\cdot\overrightarrow{b}=0~\Rightarrow~-2c^{2}-\frac{1}{2}(c^{2}-a^{2}-b^{2})=0~\Rightarrow~a^{2}+b^{2}=5c^{2}.
Примечание. Верно и обратное: если a^{2}+b^{2}=5c^{2}
, то медианы, проведённые к сторонам a
и b
, взаимно перпендикулярны (см. задачу 2343).
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 12.15, с. 290
