2343. Даны две окружности и три прямые, каждая прямая высекает на окружностях хорды равной длины. Точки пересечения прямых образуют треугольник. Докажите, что описанная окружность этого треугольника проходит через середину отрезка между центрами данных окружностей.
Решение. Лемма 1. Основание перпендикуляра, опущенного из середины линии центров двух окружностей на прямую, высекающую на этих окружностях равные хорды, лежит на радикальной оси этих окружностей.
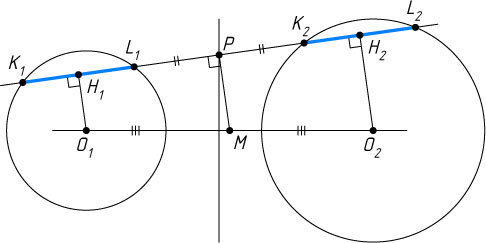
Доказательство. Пусть O_{1}
и O_{2}
— центры окружностей, H_{1}
и H_{2}
— середины высекаемых хорд K_{1}L_{1}
и K_{2}L_{2}
длины 2d
(рис. 1). Основание P
нашего перпендикуляра — середина отрезка H_{1}H_{2}
(так как отрезок O_{1}O_{2}
проектируется на H_{1}H_{2}
).
Пусть PH_{1}=PH_{2}=l
. Степень точки P
относительно первой окружности равна l^{2}-d^{2}
. Тот же результат мы получим, вычисляя степень точки P
относительно второй окружности. Следовательно, точка P
лежит на радикальной оси этих окружностей. Лемма доказана.
Лемма 2. Если основания перпендикуляров, опущенных из точки M
на стороны треугольника, лежат на одной прямой, то точка лежит на описанной окружности этого треугольника.
Доказательство. Пусть P
, Q
, R
— основания перпендикуляров, опущенных из точки M
на стороны AB
, AC
, BC
треугольника ABC
(рис. 2). Пусть точка M
не лежит на описанной окружности \Omega
треугольника ABC
. Найдём тогда такую вершину треугольника ABC
, что при гомотетии с центром в этой вершине окружность \Omega
перейдёт в окружность \Omega_{1}
, проходящую через точку M
. Такая вершина найдётся: иначе M
лежала бы на трёх касательных к \Omega
, касающихся \Omega
в вершинах треугольника ABC
, что невозможно, так как из любой точки можно провести не более двух касательных к данной окружности. (Окружности \Omega
и \Omega_{1}
касаются в вершине треугольника, поэтому окружность \Omega_{1}
может проходить через любую точку плоскости, за исключением точек, лежащих на общей касательной окружностей \Omega
и \Omega_{1}
, проведённой в этой вершине.)
Пусть найденная вершина — это A
. При нашей гомотетии треугольник ABC
перейдёт в треугольник AB_{1}C_{1}
, вписанный в \Omega_{1}
. Основания перпендикуляров, опущенных из точки M
на стороны AB_{1}
, AC_{1}
треугольника A_{1}B_{1}C_{1}
, — те же точки P
и Q
.
Пусть R_{1}
— основание перпендикуляра, опущенного из M
на B_{1}C_{1}
. Как известно, точки P
, Q
и R_{1}
лежат на одной прямой (прямая Симсона, (см. задачу 83)), а точки P
, Q
и R
лежат на одной прямой по условию. Но точки M
, R
и R_{1}
тоже будут лежать на одной прямой (так как BC
и B_{1}C_{1}
параллельны). Значит, прямая PQ
пересекает прямую MR
как в точке R
, так и в точке R_{1}
. Следовательно, точки R
и R_{1}
совпадают. Тогда совпадают и прямые AB
и A_{1}B_{1}
, т. е. коэффициент гомотетии равен 1, и \Omega_{1}
совпадает с \Omega
. Отсюда следует утверждение леммы.
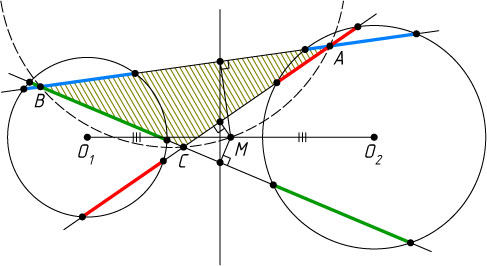
Из доказанных лемм следует, что середина отрезка с концами в центрах окружностей лежит на описанной окружности треугольника, о котором говорится в условии задачи (рис. 3).
Примечание. Прямое доказательство леммы 2 требует либо разбора нескольких случаев расположения точки M
, либо понятия ориентированного угла между прямыми.
Источник: Турнир городов. — 2007-2008, XXIX, весенний тур, старшие классы, основной вариант

