1993. Катет прямоугольного треугольника равен 2, а противолежащий ему угол равен 30^{\circ}
. Найдите расстояние между центрами окружностей, вписанных в треугольники, на которые данный треугольник делится медианой, проведённой из вершины прямого угла.
Ответ. 2\sqrt{\frac{22-12\sqrt{3}}{3}}
.
Указание. Пусть M
— середина гипотенузы AB
прямоугольного треугольника ABC
, O_{1}
и O_{2}
— центры окружностей, вписанных в треугольники AMC
и BMC
. Тогда O_{1}O_{2}
— гипотенуза прямоугольного треугольника O_{1}MO_{2}
.
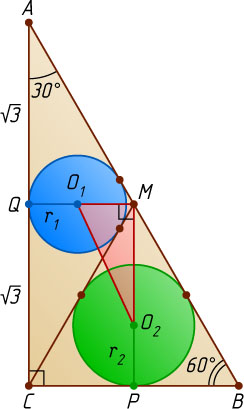
Решение. Пусть M
— середина гипотенузы AB
прямоугольного треугольника ABC
, \angle A=30^{\circ}
, BC=2
, O_{1}
и O_{2}
— центры окружностей, вписанных в треугольники AMC
и BMC
соответственно, r_{1}
и r_{2}
— радиусы этих окружностей. Тогда (см. задачу 1109)
AB=2BC=4,~CM=AM=BM=2,~AC=BC\sqrt{3}=2\sqrt{3}.
Треугольник BCM
— равносторонний, поэтому точка P
касания его вписанной окружности со стороной BC
— середина BC
, MP
— средняя линия треугольника ABC
,
MP=\frac{1}{2}AC=\sqrt{3},~MO_{2}=\frac{2}{3}MP=\frac{2}{3}\sqrt{3}.
Треугольник ACM
— равнобедренный, поэтому точка Q
касания его вписанной окружности со стороной AC
— середина AC
, MQ
— средняя линия треугольника ABC
,
MQ=\frac{1}{2}BC=1,~r_{1}=O_{1}Q=\frac{S_{\triangle AMC}}{AM+AQ}=\frac{AQ\cdot MQ}{AM+AQ}=
=\frac{\sqrt{3}\cdot1}{2+\sqrt{3}}=2\sqrt{3}-3,~MO_{1}=MQ-O_{1}Q=1-2\sqrt{3}+3=4-2\sqrt{3}.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла, поэтому MO_{1}
и MO_{2}
— биссектрисы смежных углов AMC
и BMC
, поэтому \angle O_{1}MO_{2}=90^{\circ}
, значит, O_{1}O_{2}
— гипотенуза прямоугольного треугольника O_{1}MO_{2}
. По теореме Пифагора находим, что
O_{1}O_{2}=\sqrt{MO_{2}^{2}+MO_{1}^{2}}=\sqrt{\left(\frac{2}{3}\sqrt{3}\right)^{2}+(4-2\sqrt{3})^{2}}=2\sqrt{\frac{22-12\sqrt{3}}{3}}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.13, с. 11
