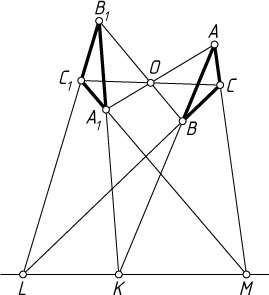
2044. Теорема Дезарга. Даны треугольники ABC
и A_{1}B_{1}C_{1}
, причём прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в одной точке или параллельны. Тогда точки пересечения прямых AB
и A_{1}B_{1}
, BC
и B_{1}C_{1}
, AC
и A_{1}C_{1}
(если они есть) лежат на одной прямой.
Указание. Примените теорему Менелая (см. задачу 1622).
Решение. Пусть прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в точке O
, прямые AB
и A_{1}B_{1}
— в точке K
, прямые BC
и B_{1}C_{1}
— в точке L
, прямые AC
и A_{1}C_{1}
— в точке M
. Применяя теорему Менелая (см. задачу 1622) к треугольнику AOB
и прямой A_{1}B_{1}
, к треугольнику AOC
и прямой A_{1}C_{1}
, к треугольнику BOC
и прямой B_{1}C_{1}
, получим, что
\frac{OA_{1}}{A_{1}A}\cdot\frac{AK}{KB}\cdot\frac{BB_{1}}{B_{1}O}=1,~\frac{OC_{1}}{C_{1}C}\cdot\frac{CM}{MA}\cdot\frac{AA_{1}}{A_{1}O}=1,~\frac{OB_{1}}{B_{1}B}\cdot\frac{BL}{LC}\cdot\frac{CC_{1}}{C_{1}O}=1.
Поэтому
1=\left(\frac{OA_{1}}{A_{1}A}\cdot\frac{AK}{KB}\cdot\frac{BB_{1}}{B_{1}O}\right)\cdot\left(\frac{OC_{1}}{C_{1}C}\cdot\frac{CM}{MA}\cdot\frac{AA_{1}}{A_{1}O}\right)\cdot\left(\frac{OB_{1}}{B_{1}B}\cdot\frac{BL}{LC}\cdot\frac{CC_{1}}{C_{1}O}\right)=
=\left(\frac{AK}{KB}\cdot\frac{BL}{LC}\cdot\frac{CM}{MA}\right)\cdot\left(\frac{OA_{1}}{A_{1}A}\cdot\frac{AA_{1}}{A_{1}O}\right)\cdot\left(\frac{BB_{1}}{B_{1}O}\cdot\frac{OB_{1}}{B_{1}B}\right)\cdot\left(\frac{OC_{1}}{C_{1}C}\cdot\frac{CC_{1}}{C_{1}O}\right)=
=\left(\frac{AK}{KB}\cdot\frac{BL}{LC}\cdot\frac{CM}{MA}\right)\cdot1\cdot1\cdot1=\frac{AK}{KB}\cdot\frac{BL}{LC}\cdot\frac{CM}{MA}.
Следовательно, точки K
, L
и M
лежат на одной прямой. Что и требовалось доказать.
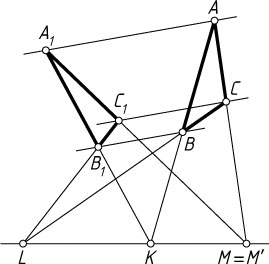
Пусть теперь прямые AA_{1}
, BB_{1}
и CC_{1}
параллельны, прямые AB
и A_{1}B_{1}
пересекаются в точке K
, прямые BC
и B_{1}C_{1}
— в точке L
, прямые AC
и A_{1}C_{1}
— в точке M
, а прямые KL
и A_{1}C_{1}
— в точке M'
. Применяя теорему Менелая к треугольнику BKL
и прямой AC
, к треугольнику B_{1}KL
и прямой A_{1}C_{1}
, получим, что
\frac{BA}{AK}\cdot\frac{KM}{ML}\cdot\frac{LC}{CB}=1,~\frac{B_{1}A_{1}}{A_{1}K}\cdot\frac{KM'}{M'L}\cdot\frac{LC_{1}}{C_{1}B_{1}}=1,
а так как \frac{BA}{AK}=\frac{B_{1}A_{1}}{A_{1}K}
и \frac{LC}{CB}=\frac{LC_{1}}{C_{1}B_{1}}
, то \frac{KM}{ML}=\frac{KM'}{M'L}
. Значит, точки M
и M'
совпадают. Отсюда следует доказываемое утверждение.
Примечание. См. также статью А.Егорова «Теоремы Чевы и Менелая», Квант, 2004, N3, с.35-38.
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 127, с. 43
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 147, с. 193
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 159, с. 17
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.78, с. 110
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2044, с. 112
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 74
Источник: Курант Р., Роббинс Г. Что такое математика?. — 2-е изд. — М.: Просвещение, 1976. — с. 200

