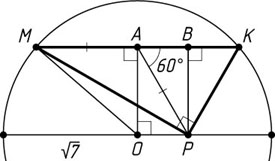
2055. Гипотенуза KM
прямоугольного треугольника KMP
является хордой окружности радиуса \sqrt{7}
. Вершина P
находится на диаметре, который параллелен гипотенузе. Расстояние от центра окружности до гипотенузы равно \sqrt{3}
. Найдите острые углы треугольника KMP
.
Ответ. 30^{\circ}
, 60^{\circ}
.
Указание. Пусть O
— центр окружности, A
— середина KM
. Рассмотрите треугольник OAM
.
Решение. Пусть O
— центр данной окружности, OA
— перпендикуляр к гипотенузе. Тогда A
— середина гипотенузы. Из прямоугольного треугольника OMA
по теореме Пифагора находим, что
AM^{2}=OM^{2}-OA^{2}=7-3=4.
Значит, AP=AK=AM=2
(см. задачу 1109).
Пусть PB
— высота треугольника KMP
. Тогда PB=OA=\sqrt{3}
. Поэтому
\sin\angle KAP=\frac{PB}{AP}=\frac{\sqrt{3}}{2}.
Следовательно, \angle KAP=60^{\circ}
, а так как треугольник KAP
равносторонний, то \angle MKP=60^{\circ}
.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1988, вариант 2, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 32
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.20, с. 12
