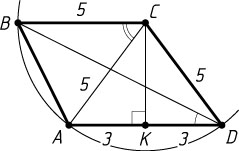
2095. В трапеции ABCD
(AD\parallel BC
) угол ADB
в два раза меньше угла ACB
. Известно, что BC=AC=5
и AD=6
. Найдите площадь трапеции.
Ответ. 22.
Указание. Точки A
, B
и D
лежат на окружности с центром C
и радиусом 5.
Решение. Построим окружность с центром в точке C
и радиусом CB=CA=5
. Поскольку \angle ADB=\frac{1}{2}\angle ACB
, то точка D
принадлежит этой окружности (см. задачу 2900), и CD=CA=5
.
Пусть CK
— высота равнобедренного треугольника ACD
. Тогда
CK=\sqrt{AC^{2}-AK^{2}}=\sqrt{25-9}=4.
Поскольку CK
— высота трапеции ABCD
, то
S_{ABCD}=\frac{AD+BC}{2}\cdot CK=\frac{6+5}{2}\cdot4=22.
Источник: Вступительный экзамен в МФТИ. — 1985, № 4, билет 10, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 85-10-4, с. 270
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.31, с. 32
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4.47.2, с. 50
