2149. На продолжении стороны AD
ромба ABCD
за точку D
взята точка K
. Прямые AC
и BK
пересекаются в точке Q
. Известно, что AK=14
и что точки A
, B
и Q
лежат на окружности радиуса 6, центр которой принадлежит отрезку AK
. Найдите BK
.
Ответ. 7.
Указание. Пусть O
— центр окружности. Воспользуйтесь подобием треугольников KQO
и KBA
.
Решение. Пусть O
— центр окружности, F
— вторая точка пересечения окружности с прямой AK
. Поскольку треугольник AOQ
— равнобедренный (OA=OQ=6
), то \angle AQO=\angle OAQ=\angle BAQ
. Поэтому OQ\parallel AB
. Следовательно, треугольники KQO
и KBA
подобны. Значит, \frac{OQ}{AB}=\frac{OK}{AK}
. Отсюда находим, что
AB=\frac{OQ\cdot AK}{OK}=\frac{6\cdot14}{14-6}=\frac{21}{2}.
Поскольку AQ
— биссектриса треугольника BAK
, то
\frac{BQ}{KQ}=\frac{AB}{AK}=\frac{3}{4}.
Кроме того,
KQ\cdot KB=KF\cdot KA,~\mbox{или}~KQ\cdot KB=2\cdot14=28
(см. задачу 2636), а так как
BK=KQ+QB=KQ+\frac{3}{4}KQ=\frac{7}{4}KQ,
то
KQ^{2}=\frac{4\cdot28}{7}=16,~KQ=4,~BQ=3,~BK=7.
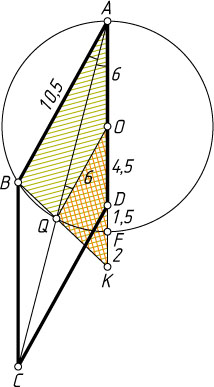
Источник: Вступительный экзамен в МФТИ. — 1990, билет 1, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 90-1-4, с. 301
