2174. Прямая, параллельная гипотенузе AB
прямоугольного треугольника ABC
, пересекает катет AC
в точке D
, а катет BC
— в точке E
, причём DE=2
, а BE=1
. На гипотенузе взята точка F
, причём BF=1
. Известно также, что \angle FCB=\alpha
. Найдите площадь треугольника ABC
.
Ответ. \frac{1}{2}(1+2\cos2\alpha)^{2}\tg2\alpha
.
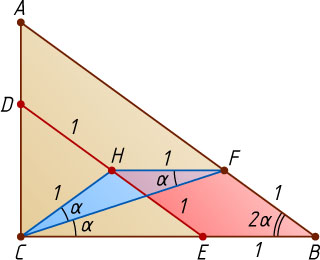
Указание. Пусть H
— середина DE
. Тогда треугольник CHF
— равнобедренный.
Решение. Пусть H
— середина DE
. Тогда HFBE
— параллелограмм (даже ромб). Поэтому HF=BE=1
.
Поскольку CH=\frac{1}{2}DE=1
(см. задачу 1109), то треугольник CHF
равнобедренный. Поэтому
\angle HCF=\angle HFC=\angle FCB=\alpha,~\angle HCB=2\alpha.
Тогда
\angle B=\angle DEC=\angle HCB=2\alpha.
Следовательно,
CE=DE\cos\angle DEC=2\cos2\alpha,~BC=CE+EB=2\cos2\alpha+1,
AC=BC\tg\angle ABC=BC\tg2\alpha=(2\cos2\alpha+1)\tg2\alpha.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}BC\cdot AC=\frac{1}{2}(2\cos2\alpha+1)^{2}\tg2\alpha.
Источник: Вступительный экзамен на физический факультет МГУ. — 1983, № 5, вариант 1
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 36
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.18, с. 11
