2201. Одна окружность лежит внутри другой. Пусть для некоторой точки A
большей окружности верно следующее утверждение: если из точки A
проведена её хорда AB
, касающаяся меньшей окружности, а из точки B
проведена хорда BC
большей окружности, отличная от AB
и касающаяся меньшей окружности, то хорда AC
касается меньшей окружности. Тогда оно верно для произвольной точки большей окружности (теорема Понселе для треугольника).
Какую траекторию описывает точка пересечения: а) медиан; б) высот всех таких треугольников ABC
?
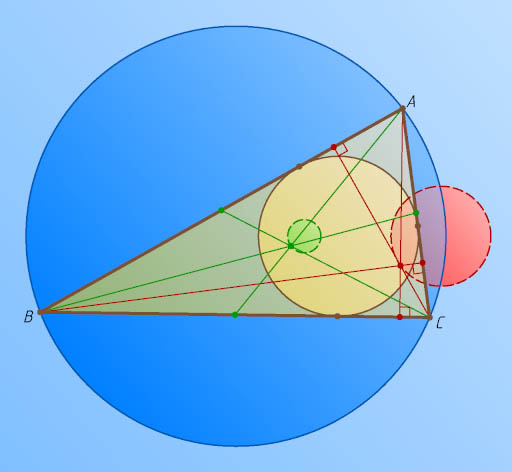
Ответ. а) Окружность, гомотетичная с центром O
и коэффициентом \frac{2}{3}
окружности с центром I
радиуса \frac{R}{2}-r
, где O
и I
— центры соответственно большей и меньшей окружностей, а R
и r
— их радиусы;
б) окружность, гомотетичная с центром O
и коэффициентом 2 окружности с центром I
радиуса \frac{R}{2}-r
;
Решение. Докажем сначала теорему Понселе для треугольника. Пусть I
и O
— центры окружностей радиусов r
и R
соответственно. Первая из этих окружностей вписана в треугольник ABC
, а вторая описана около этого треугольника. По формуле Эйлера (см. задачу 126) OI^{2}=R^{2}-2Rr
.
Из произвольной точки X
большей окружности проведём различные хорды XY
и XZ
большей окружности, касающиеся меньшей. Предположим, что хорда YZ
не имеет общих точек с меньшей окружностью. Будем увеличивать угол YXZ
так, чтобы луч XI
оставался его биссектрисой. Тогда расстояние от точки I
до хорд XY
и XZ
будет увеличиваться (это расстояние равно XI\sin\frac{\alpha}{2}
, где \alpha=\angle YXZ
), а до хорды YZ
уменьшаться.
В какой-то момент хорда YZ
коснётся меньшей окружности. При этом расстояние OI
и радиус R
большей окружности не изменятся. Из формулы Эйлера следует, что не изменится и радиус меньшей окружности. Получено противоречие.
Аналогично, если предположить, что хорда YZ
пересекает меньшую окружность. Следовательно, треугольник XYZ
, вписанный в большую окружность, оказывается описанным около меньшей. Что и требовалось доказать.
Пусть H
— ортоцентр треугольника ABC
, M
— точка пересечения медиан, O_{1}
— центр окружности, проходящей через середины сторон треугольника ABC
(окружность девяти точек). Тогда O_{1}
— середина отрезка OH
, а радиус этой окружности равен \frac{R}{2}
.
По теореме Фейербаха вписанная окружность треугольника ABC
касается окружности, проходящей через середины его сторон. Расстояние между центрами касающихся внутренним образом окружностей равно разности их радиусов, значит, IO_{1}=\frac{R}{2}-r
. Следовательно, точка O_{1}
лежит на окружности \omega
с центром I
и радиусом \frac{R}{2}-r
.
Поскольку OH=2OO_{1}
, точка H
лежит на окружности, гомотетичной с центром O
и коэффициентом 2 окружности \omega
.
Точка M
лежит на прямой OH
(прямая Эйлера) между O
и H
и делит отрезок OH
в отношении 1:2
, считая от точки O
. Значит, OM:OO_{1}=\frac{\frac{1}{3}OH}{\frac{1}{2}OH}=\frac{2}{3}
. Следовательно, точка M
лежит на окружности, гомотетичной с центром O
и коэффициентом \frac{2}{3}
окружности \omega
.
Источник: Математика в задачах: Сб. материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду / Под ред. А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова и др. — М.: МЦНМО, 2009. — № 3(а,б), с. 163
