2212. В прямоугольном треугольнике ABC
из вершины прямого угла C
проведены биссектриса CL
и медиана CM
. Найдите площадь треугольника ABC
, если LM=a
, CM=b
.
Ответ. \frac{b^{2}(b^{2}-a^{2})}{a^{2}+b^{2}}
.
Указание. Воспользуйтесь свойством биссектрисы треугольника и составьте систему уравнений относительно x
и y
, где x
и y
— катеты треугольника.
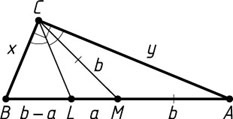
Решение. Заметим, что AM=MB=b
(см. задачу 1109). Обозначим BC=x
, AC=y
. Пусть x\lt y
. Тогда по свойству биссектрисы треугольника
\frac{x}{y}=\frac{BL}{AL}=\frac{b-a}{b+a}.
С другой стороны, по теореме Пифагора
BC^{2}+AC^{2}=AB^{2},~\mbox{или}~x^{2}+y^{2}=4b^{2}.
Решив систему уравнений
\syst{\frac{x}{y}=\frac{b-a}{b+a}\\x^{2}+y^{2}=4b^{2},\\}
получим, что
x=\frac{\sqrt{2}b(b-a)}{\sqrt{a^{2}+b^{2}}},~y=\frac{\sqrt{2}b(b+a)}{\sqrt{a^{2}+b^{2}}}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}xy=\frac{b^{2}(b^{2}-a^{2})}{a^{2}+b^{2}}.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1973, вариант 1, № 3
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 167, с. 20
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 229
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.7, с. 10
