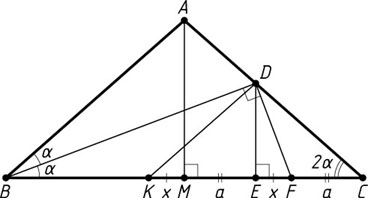
2218. В треугольнике ABC
известно, что AB=AC
и угол BAC
— тупой. Пусть D
— точка пересечения биссектрисы угла ABC
со стороной AC
, M
— основание перпендикуляра, опущенного из A
на сторону BC
, E
— основание перпендикуляра, опущенного из D
на сторону BC
. Через точку D
проведён также перпендикуляр к BD
до пересечения со стороной BC
в точке F
. Известно, что ME=FC=a
. Найдите площадь треугольника ABC
.
Ответ. \frac{25a^{2}\sqrt{7}}{12}
.
Указание. Обозначьте EF=x
, выразите через a
и x
отрезки AB
, AM
и BM
, и примените теорему Пифагора к треугольнику ABM
.
Решение. Первый способ. Обозначим EF=x
. По теореме о пропорциональных отрезках и свойству биссектрисы треугольника
\frac{EM}{EC}=\frac{AD}{DC}=\frac{AB}{BC},~\mbox{или}~\frac{a}{a+x}=\frac{AB}{2(2a+x)},
откуда AB=\frac{2a(2a+x)}{a+x}
. Из прямоугольного треугольника BDF
находим, что
DE^{2}=BE\cdot EF=(3a+x)x.
Поэтому DE=\sqrt{(3a+x)x}
. Поскольку треугольники AMC
и DEC
подобны, то
AM=\frac{DE\cdot MC}{EC}=\frac{(2a+x)\sqrt{(3a+x)x}}{a+x}.
По теореме Пифагора
AB^{2}=BM^{2}+AM^{2}~\Rightarrow
\Rightarrow~\frac{4a^{2}(2a+x)^{2}}{(x+a)^{2}}=(2a+x)^{2}+\frac{(2a+x)^{2}x(3a+x)}{(x+a)^{2}}~\Rightarrow
\Rightarrow~2x^{2}+5ax-3a^{2}=0.
Отсюда находим, что
x=\frac{a}{2},~BM=\frac{5x}{2},~AM=\frac{5a\sqrt{7}}{6}.
Следовательно,
S_{\triangle ABC}=BM\cdot AM=\frac{25a^{2}\sqrt{7}}{12}.
Второй способ. Обозначим EF=x
, \angle ACB=\angle ABC=2\alpha
. Пусть K
— середина отрезка BF
. Тогда DK
— медиана прямоугольного треугольника BDF
. Значит (см. задачу 1109),
BK=KD=KF,~\angle DKC=2\angle DBK=2\alpha=\angle ACB.
Поэтому треугольник CDK
— равнобедренный. Его высота DE
является медианой, значит,
KM+ME=EF+FC,~\mbox{или}~KM+a=x+a.
Следовательно, KM=x
. Тогда
BK=KF=2x+a,~BM=BK+KM=(2x+a)+x=3x+a,
MC=ME+EF+FC=a+x+a=2a+x,
а так как BM=MC
, то 3x+a=2a+x
. Отсюда находим, что x=\frac{a}{2}
. Тогда
CD=DK=BK=2x+a=a+a=2a.
Из прямоугольного треугольника CED
находим, что
\cos2\alpha=\frac{CE}{CD}=\frac{x+a}{2a}=\frac{\frac{3a}{2}}{2a}=\frac{3}{4}.
Тогда
\tg2\alpha=\sqrt{\frac{1}{\cos^{2}2\alpha}-1}=\sqrt{\frac{16}{9}-1}=\frac{\sqrt{7}}{3},
AM=MC\tg2\alpha=(2a+x)\tg2\alpha=\frac{5a}{2}\cdot\frac{\sqrt{7}}{3}=\frac{5a\sqrt{7}}{6}.
Следовательно,
S_{\triangle ABC}=MC\cdot AM=\frac{5a}{2}\cdot\frac{5a\sqrt{7}}{6}=\frac{25a^{2}\sqrt{7}}{12}.
Третий способ. Пусть N
— точка пересечения прямых AB
и DF
, а L
— точка пересечения прямой, проведённой через точку D
параллельно BC
, со стороной AB
.
Треугольник BLD
равнобедренный (BL=LD
), так как
\angle BDL=\angle DBC=\angle LBD,
Значит, CD=BL=DL
.
Треугольник FBN
также равнобедренный (BF=BN
), так как его биссектриса BD
является высотой. Значит, D
— середина NF
, а DL
— средняя линия треугольника BNF
. Пусть K
— точка пересечения AM
и DL
. Тогда DKME
— прямоугольник, поэтому
KD=ME=a,~DL=2KD=2a,~BF=2DL=4a,
BC=BF+FC=4a+a=5a,~BE=BM+ME=\frac{5}{2}a+a=\frac{7}{2}a,
EF=BF-BE=4a-\frac{7}{2}a=\frac{1}{2}a,~CE=a+\frac{1}{2}a=\frac{3}{2}a,
а так как CD=BL=2a
, то из прямоугольного треугольника CED
находим, что
DE=\sqrt{CD^{2}-CE^{2}}=\sqrt{4a^{2}-\frac{9}{4}a^{2}}=\frac{a\sqrt{7}}{2}.
Треугольник AMC
подобен треугольнику DEC
с коэффициентом
k=\frac{CM}{CE}=\frac{\frac{5}{2}a}{\frac{3}{2}a}=\frac{5}{3},
Значит,
AM=\frac{5}{3}DE=\frac{5}{3}\cdot\frac{a\sqrt{7}}{2}=\frac{5a\sqrt{7}}{6}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}BC\cdot AM=\frac{5}{2}a\cdot\frac{5a\sqrt{7}}{6}=\frac{25a^{2}\sqrt{7}}{12}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1975, вариант 1, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 211
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.25, с. 12
