2245. В треугольнике ABC
известно, что AB=2
, AC=5
, BC=6
. Найдите расстояние от вершины B
до точки пересечения высот.
Ответ. \frac{25}{\sqrt{39}}
.
Указание. Расстояние BH
от вершины B
до точки H
пересечения высот треугольника ABC
равно удвоенному расстоянию от центра O
описанной окружности до стороны AC
(см. задачу 1257).
Решение. По теореме косинусов находим, что
\cos\angle B=\frac{AB^{2}+BC^{2}-AC^{2}}{2AB\cdot BC}=\frac{4+36-25}{2\cdot2\cdot6}=\frac{5}{8}.
Тогда
\sin\angle B=\sqrt{1-\cos^{2}\angle B}=\sqrt{1-\left(\frac{5}{8}\right)^{2}}=\frac{\sqrt{39}}{8}.
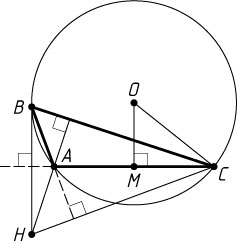
Пусть O
— центр описанной окружности треугольника ABC
, R
— её радиус, M
— проекция центра на сторону AC
. Тогда BH=2OM
(см. задачу 1257). По теореме синусов
AO=R=\frac{AC}{2\sin\angle B}=\frac{5}{2\cdot\frac{\sqrt{39}}{8}}=\frac{20}{\sqrt{39}}.
Следовательно,
BH=2OM=\sqrt{AO^{2}-AM^{2}}=2\sqrt{AO^{2}-\frac{AC^{2}}{4}}=
=2\sqrt{\frac{400}{39}-\frac{25}{4}}=\frac{25}{\sqrt{39}}.
Источник: Вступительный экзамен в МФТИ. — 1966, билет 3, № 1
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 66-3-1, с. 115
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.13, с. 123
