2273. На сторонах AB
и BC
треугольника ABC
отмечены точки D
и F
соответственно, E
— середина отрезка DF
. Докажите, что AD+FC\leqslant AE+EC
.
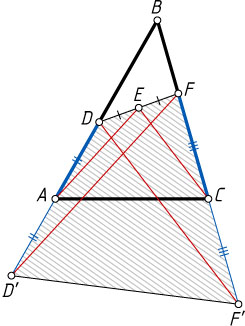
Решение. Первый способ. Пусть D'
— точка, симметричная точке D
относительно точки A
, а F'
— симметрична точке F
относительно точки C
. Тогда DD'=2AD
, FF'=2FC
, а так как AE
и CE
— средние линии треугольников FDD'
и DFF'
, то FD'=2AE
и DF'=2EC
.
Известно, что сумма диагоналей выпуклого четырёхугольника больше суммы двух противоположных сторон, поэтому FD'+DF'\gt DD'+FF'
, или 2AE+2EC\gt2AD+2FC
. Следовательно, AD+FC\lt AE+EC
. (Если точка D
совпадает с A
, а F
совпадает с C
, то AD+FC=AE+EC
.)
Второй способ. Проведём отрезок BE
. Применив неравенство треугольника к треугольникам AEB
и BEC
, получим
AE+BE\gt AD+DB,~CE+BE\gt CF+BF.
Сложив почленно эти неравенства и учитывая известное неравенство
BE\lt\frac{BD+BF}{2}
для медианы треугольника (см. задачу 3504), получим
AE+CE+2BE\gt AD+DB+CF+BF\gt AD+DB+2BE.
Следовательно,
AE+CE\gt AD+CF.
Что и требовалось доказать.
Автор: Берлов С. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1993, отборочный тур, 11 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 93.60
Источник: Московская математическая регата. — 2019-2020, четвёртый тур, № 2, 10 класс
