2293. Дан треугольник ABC
. Точки M_{1}
, M_{2}
, M_{3}
— середины сторон AB
, BC
и AC
, а точки H_{1}
, H_{2}
, H_{3}
— основания высот, лежащие на тех же сторонах. Докажите, что из отрезков H_{1}M_{2}
, H_{2}M_{3}
и H_{3}M_{1}
можно построить треугольник.
Указание. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.
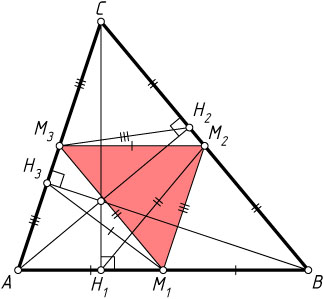
Решение. Указанные отрезки равны половинам сторон треугольника ABC
(например, медиана H_{1}M_{2}
прямоугольного треугольника BH_{1}C
равна половине гипотенузы BC
, см. задачу 1109). Поэтому из них можно построить треугольник, стороны которого вдвое меньше соответствующих сторон треугольника ABC
, т. е. треугольник, равный треугольнику M_{1}M_{2}M_{3}
.
Автор: Гальперин Г. А.
Источник: Турнир городов. — 2005-2006, XXVII, осенний тур, младшие классы, тренировочный вариант
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 1.34, с. 14
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 1.34.1, с. 14
