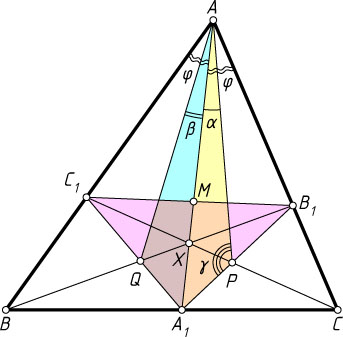
2300. На биссектрисе AA_{1}
треугольника ABC
выбрана точка X
. Прямая BX
пересекает сторону AC
в точке B_{1}
, а прямая CX
пересекает сторону AB
в точке C_{1}
. Отрезки A_{1}B_{1}
и CC_{1}
пересекаются в точке P
, а отрезки A_{1}C_{1}
и BB_{1}
пересекаются в точке Q
. Докажите, что углы PAC
и QAB
равны.
Указание. Применяя теорему Чевы к треугольнику A_{1}B_{1}C_{1}
, свойство биссектрисы и теорему синусов (к треугольникам APA_{1}
и APB_{1}
), докажите, что \frac{\sin\angle A_{1}AP}{\sin\angle B_{1}AP}=\frac{A_{1}P}{AA_{1}}\cdot\frac{AB_{1}}{B_{1}P}
и \frac{\sin\angle A_{1}AQ}{\sin\angle C_{1}AQ}=\frac{A_{1}Q}{AA_{1}}\cdot\frac{AC_{1}}{C_{1}Q}
.
Решение. Обозначим
\angle A_{1}AC=\angle A_{1}AB=\varphi\lt\frac{\pi}{2},~\angle A_{1}AP=\alpha,~\angle A_{1}AQ=\beta,~\angle APA_{1}=\gamma.
Лемма.
\frac{\sin\alpha}{\sin(\varphi-\alpha)}=\frac{A_{1}P}{AA_{1}}\cdot\frac{AB_{1}}{B_{1}P},~\frac{\sin\beta}{\sin(\varphi-\beta)}=\frac{A_{1}Q}{AA_{1}}\cdot\frac{AC_{1}}{C_{1}Q}.
Доказательство. Пусть M
— точка пересечения AA_{1}
и B_{1}C_{1}
. Применяя теорему Чевы (см. задачу 1621) к треугольнику A_{1}B_{1}C_{1}
, получим, что
\frac{A_{1}P}{PB_{1}}\cdot\frac{B_{1}M}{MC_{1}}\cdot\frac{C_{1}Q}{QA_{1}}=1,
а так как по свойству биссектрисы треугольника \frac{B_{1}M}{MC_{1}}=\frac{AB_{1}}{AC_{1}}
, то
\frac{A_{1}P}{PB_{1}}\cdot\frac{AB_{1}}{AC_{1}}\cdot\frac{C_{1}Q}{QA_{1}}=1,
откуда
\frac{A_{1}P\cdot AB_{1}}{PB_{1}}=\frac{A_{1}Q\cdot AC_{1}}{C_{1}Q}.
Применяя теорему синусов в треугольникам APA_{1}
и APB_{1}
, получим, что
\frac{\sin\alpha}{\sin\gamma}=\frac{A_{1}P}{AA_{1}},~\frac{\sin(180^{\circ}-\gamma)}{\sin(\varphi-\alpha)}=\frac{AB_{1}}{B_{1}P},
откуда
\frac{\sin\alpha}{\sin(\varphi-\alpha)}=\frac{A_{1}P}{AA_{1}}\cdot\frac{AB_{1}}{B_{1}P}.
Аналогично
\frac{\sin\beta}{\sin(\varphi-\beta)}=\frac{A_{1}Q}{AA_{1}}\cdot\frac{AC_{1}}{C_{1}Q},
Лемма доказана.
Поскольку
\frac{A_{1}P\cdot AB_{1}}{PB_{1}}=\frac{A_{1}Q\cdot AC_{1}}{C_{1}Q},
из леммы следует, что \frac{\sin\alpha}{\sin(\varphi-\alpha)}=\frac{\sin\beta}{\sin(\varphi-\beta)}
.
Функция f(x)=\frac{\sin x}{\sin(\varphi-x)}
возрастает на промежутке (0;\varphi)
(числитель и знаменатель на этом промежутке положительны, причём числитель возрастает, а знаменатель убывает), поэтому каждое своё значение на этом промежутке она принимает ровно один раз. Из равенства \frac{\sin\alpha}{\sin(\varphi-\alpha)}=\frac{\sin\beta}{\sin(\varphi-\beta)}
следует, что \alpha=\beta
. Значит, \angle PAC=\angle QAB
.
Автор: Волчкевич М. А.
Источник: Турнир городов. — 2005-2006, XXVII, весенний тур, старшие классы, основной вариант
