2304. На стороне BC
треугольника ABC
отмечена точка K
. В треугольники ABK
и ACK
вписаны окружности. Первая касается стороны BC
в точке M
, вторая — в точке N
. Докажите, что BM\cdot CN\gt KM\cdot KN
.
Решение. Пусть p_{1}
и p_{2}
— полупериметры треугольников ABK
и ACK
соответственно. Обозначим
BC=a,~AC=b,~AB=c,~BK=c',~KC=b',~AK=d.
Тогда
BM=p_{1}-AK=\frac{c+c'-d}{2},~CN=p_{2}-AK=\frac{b+b'-d}{2},
KM=p_{1}-AB=\frac{d+c'-c}{2},~KN=p_{2}-AK=\frac{d+b'-b}{2}
(см. задачу 219), поэтому
BM\cdot CN\gt KM\cdot KN~\Leftrightarrow
\Leftrightarrow~\frac{c+c'-d}{2}\cdot\frac{b+b'-d}{2}\gt\frac{d+c'-c}{2}\cdot\frac{d+b'-b}{2}~\Leftrightarrow
\Leftrightarrow~(c+c'-d)(b+b'-d)\gt(d+c'-c)(d+b'-b)~\Leftrightarrow
\Leftrightarrow~d^{2}-d(b+c+b'+c')+(b+b')(c+c')\gt d^{2}+d(b'-b+c'-c)+(c'-c)(b'-b)~\Leftrightarrow
\Leftrightarrow~(c+c')(b+b')-(c'-c)(b'-b)\gt d(b'-b+c'-c+b+c+b'+c')~\Leftrightarrow
\Leftrightarrow~2b'c+2bc'\gt2d(b'+c')~\Leftrightarrow~b'c+bc'\gt da~\Leftrightarrow~c\cdot\frac{b'}{a}+b\cdot\frac{c'}{a}\gt d.
Через точку K
проведём прямую, параллельную AB
. Пусть эта прямая пересекает сторону AC
в точке P
. Тогда
KP=AB\cdot\frac{CK}{BC}=c\cdot\frac{b'}{a},~AP=AC\cdot\frac{BK}{BC}=b\cdot\frac{c'}{a}.
Поэтому
c\cdot\frac{b'}{a}+b\cdot\frac{c'}{a}\gt d~\Leftrightarrow~KP+AP\gt AK.
Последнее неравенство — неравенство треугольника для треугольника AKP
. Следовательно, BM\cdot CN\gt KM\cdot KN
.
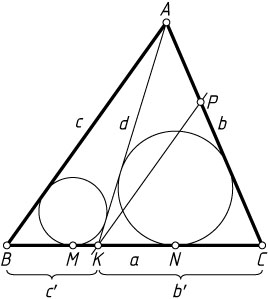
Автор: Маркелов С. В.
Источник: Турнир городов. — 2004-2005, XXVI, осенний тур, младшие классы, основной вариант
