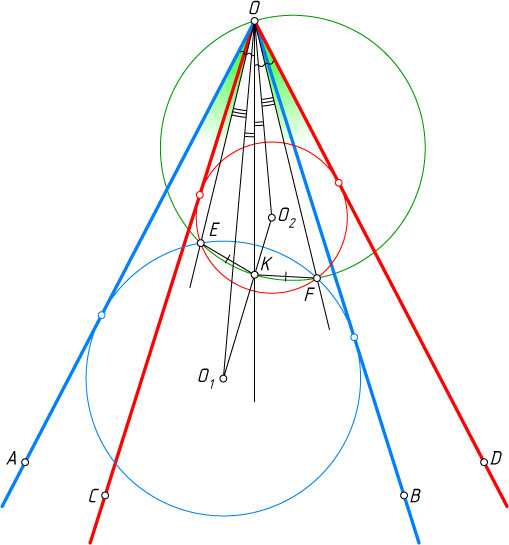
2306. Углы AOB
и COD
совмещаются поворотом так, что луч OA
совмещается лучом OC
, луч OB
— с лучом OD
. В них вписаны окружности, пересекающиеся в точках E
и F
. Докажите, что углы AOE
и DOF
равны.
Решение. Пусть O_{1}
и O_{2}
— центры окружностей, вписанных в углы AOB
и DOC
соответственно, r_{1}
и r_{2}
— радиусы окружностей. Если r_{1}=r_{2}
, то утверждение очевидно. Предположим, что r_{1}\ne r_{2}
.
Проведём биссектрису угла AOD
. Пусть она пересекает отрезок O_{1}O_{2}
в точке K
. Тогда
\angle KOO_{1}=\angle AOK-\angle AOO_{1}=\angle DOK-\angle DOO_{2}=\angle KOO_{2},
значит, луч OK
— биссектриса треугольника O_{1}OO_{2}
. По свойству биссектрисы треугольника \frac{KO_{1}}{KO_{2}}=\frac{OO_{1}}{OO_{2}}
.
Обозначим \angle AOB=\angle COD=\alpha
. Тогда OO_{1}=\frac{r_{1}}{\sin\frac{\alpha}{2}}
и OO_{2}=\frac{r_{2}}{\sin\frac{\alpha}{2}}
, поэтому \frac{OO_{1}}{OO_{2}}=\frac{r_{1}}{r_{2}}
. Значит,
\frac{KO_{1}}{KO_{2}}=\frac{OO_{1}}{OO_{2}}=\frac{r_{1}}{r_{2}}.
Кроме того, \frac{EO_{1}}{EO_{2}}=\frac{FO_{2}}{FO_{2}}=\frac{r_{1}}{r_{2}}
. Таким образом отношение расстояний от точек O
, K
, E
и F
до концов отрезка O_{1}O_{2}
одно и то же (\frac{r_{1}}{r_{2}}\ne1
). Следовательно, точки O
, K
, E
и F
лежат на одной окружности — окружности Аполлония (см. задачу 2444). Вписанные в эту окружность углы KOE
и KOF
опираются на равные хорды (EK=FK
, так как точка K
лежит на серединном перпендикуляре O_{1}O_{2}
к общей хорде EF
данных окружностей). Следовательно, эти углы равны. Тогда равны и углы AOE
и DOF
. Что и требовалось доказать.
Автор: Кожевников П. А.
Автор: Богданов И. И.
Источник: Турнир городов. — 2004-2005, XXVI, осенний тур, старшие классы, основной вариант
