2314. Окружности \Omega_{1}
и \Omega_{2}
пересекаются в точках A
и B
. Через точку B
проведена прямая, вторично пересекающая окружности \Omega_{1}
и \Omega_{2}
в точках K
и M
. Прямая l_{1}
касается окружности \Omega_{1}
в точке Q
и параллельна AM
. Прямая QA
вторично пересекает окружность \Omega_{2}
в точке R
. Докажите, что:
а) касательная l_{2}
, проведённая к окружности \Omega_{2}
в точке R
, параллельна AK
;
б) прямые l_{1}
, l_{2}
и KM
имеют общую точку.
Решение. Рассмотрим случай, изображённый на рисунке. Пусть прямые MK
и l_{1}
пересекаются в точке P
. Прямые AM
и PQ
параллельны, поэтому \angle AMP=\angle MPQ
. Вписанные в окружность \Omega_{2}
углы ARB
и AMB
опираются на одну и ту же дугу, поэтому \angle ARB=\angle AMB
. Тогда
\angle BPQ=\angle MPQ=\angle AMB=\angle ARB=\angle BRQ.
Из точек P
и R
, лежащих по одну сторону от прямой BQ
, отрезок BQ
виден под одним и тем же углом, значит, точки P
, R
, Q
и B
лежат на одной окружности. Вписанные в эту окружность углы PRQ
и PBQ
опираются на одну и ту же дугу. Вписанные в окружность \Omega_{1}
углы KAQ
и KBQ
также опираются на одну и ту же дугу. Значит,
\angle KAQ=\angle KBQ=\angle PBQ=\angle PRQ.
Следовательно, AK\parallel PR
.
Докажем, что прямая PR
касается окружности \Omega_{2}
. Отсюда будет следовать решение обоих пунктов нашей задачи (точка P
будет общей точкой прямых l_{1}
, l_{2}
и KM
).
Достаточно доказать, что \angle ARP=\angle ABR
. Тогда из теоремы, обратной теореме об угле между касательной и хордой (см. задачу 144), будет следовать, что прямая PR
, параллельная AK
, касается окружности \Omega_{2}
.
В свою очередь, равенство этих углов равносильно равенству углов ABQ
и KBR
, а так как \angle ABQ=180^{\circ}-\angle AKQ
и \angle KBR=180^{\circ}-\angle MBR
, то достаточно доказать, что \angle AKQ=\angle MBR
.
Докажем это равенство. Пусть T
— точка на продолжении PQ
за точку Q
. Из теоремы об угле между касательной и хордой и параллельности прямых PQ
и AM
следует, что
\angle AKQ=\angle AQT=180^{\circ}-\angle QAM=\angle MAR=\angle MBR.
Что и требовалось доказать. Аналогично для остальных случаев
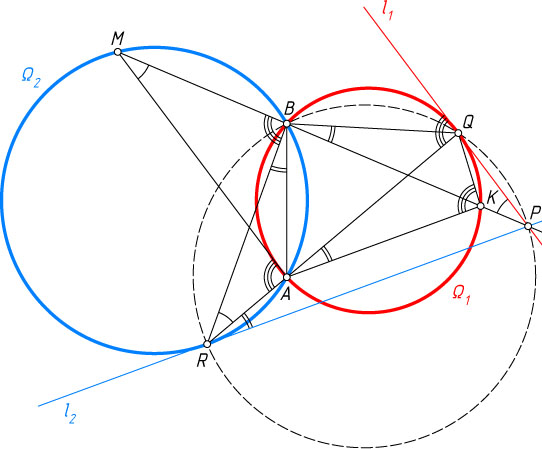
Примечание. Разбора всех возможных случаев можно избежать, если рассматривать ориентированные углы.
Автор: Протасов В. Ю.
Источник: Турнир городов. — 2002-2003, XXIV, осенний тур, старшие классы, основной вариант
