2315. На боковых сторонах AB
и BC
равнобедренного треугольника ABC
взяли соответственно точки K
и L
так, что AK+LC=KL
. Из середины M
отрезка KL
провели прямую, параллельную BC
, и эта прямая пересекла сторону AC
в точке N
. Найдите величину угла KNL
.
Ответ. 90^{\circ}
.
Указание. Через точку K
проведите прямую, параллельную BC
.
Решение. Пусть прямая, проходящая через точку K
параллельно BC
, пересекает основание AC
в точке P
. Треугольник AKP
равнобедренный, поэтому
KP=AK,~KP+LC=AK+LC=KL.
Отрезок MN
— средняя линия трапеции (или параллелограмма) KPCL
, поэтому MN=\frac{KP+LC}{2}=\frac{KL}{2}
.
Медиана NM
треугольника KNL
равна половине стороны KL
, значит, треугольник KNL
прямоугольный (см. задачу 1188), \angle KNL=90^{\circ}
.
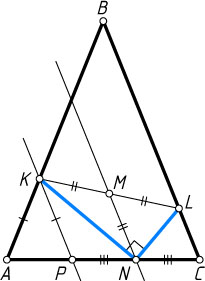
Автор: Женодаров Р. Г.
Источник: Турнир городов. — 2002-2003, XXIV, весенний тур, младшие классы, тренировочный вариант
