2318. Трапеция с основаниями AD
и BC
описана вокруг окружности, E
— точка пересечения диагоналей. Докажите, что угол AED
не может быть острым.
Указание. Окружности, построенные на боковых сторонах AB
и CD
трапеции как на диаметрах, касаются внешним образом.
Решение. На боковых сторонах AB
и CD
трапеции построим как на диаметрах окружности. Расстояние между их центрами равно средней линии MN
трапеции, а так как трапеция описанная, то
MN=\frac{1}{2}(AD+BC)=\frac{1}{2}(AB+CD)=\frac{1}{2}AB+\frac{1}{2}CD=AM+DN,
т. е. расстояние между центрами окружностей равно сумме их радиусов. Следовательно, окружности касаются внешним образом.
Из каждой точки, лежащей внутри одной из окружностей, диаметр виден под тупым углом, а из точки, лежащей вне окружности, — под острым. Из точки E
диаметры AB
и CD
видны под равными углами, значит, эта точка не может лежать внутри одной из окружностей, так как тогда один из углов AEB
и CED
был бы острым, а второй — тупым (см. задачу 1772). Значит, эти углы не больше 90^{\circ}
. Следовательно, дополнительный к ним угол AED
не меньше 90^{\circ}
.
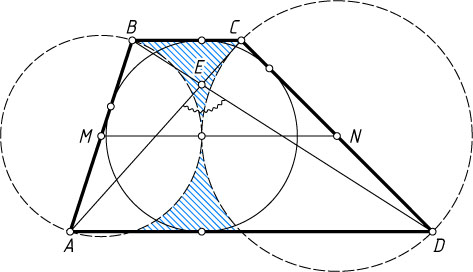
Примечание. Окружности, построенные на боковых сторонах AB
и CD
трапеции как на диаметрах, касаются в центре вписанной окружности трапеции (но в решении задачи это не понадобилось).
Заметим, что угол AED
не может быть прямым, так как в этом случае диагонали трапеции пересекались бы в центре вписанной окружности, а тогда ABCD
— ромб, а значит, не трапеция.
Автор: Заславский А. А.
Источник: Турнир городов. — 2002-2003, XXIV, весенний тур, младшие классы, основной вариант
Источник: Московская математическая регата. — 2016-2017, четвёртый тур, № 2, 10 класс
