2335. Середина одной из сторон треугольника и основания высот, опущенных на две другие стороны, образуют равносторонний треугольник. Верно ли, что исходный треугольник тоже равносторонний?
Ответ. Неверно.
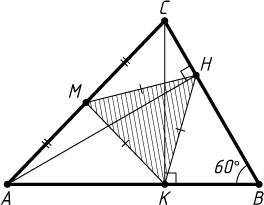
Решение. Первый способ. Рассмотрим произвольный остроугольный треугольник ABC
, где \angle B=60^{\circ}
. Пусть AH
и CK
— высоты, M
— середина AC
.
В прямоугольных треугольниках AHC
и AKC
медианы HM
и KM
равны половине гипотенузы (см. задачу 1109), поэтому треугольники CMH
и AMK
равнобедренные. Угол AMH
— внешний угол треугольника CMH
, и значит, равен 2\angle C
, а угол CMK
— внешний угол треугольника AMK
, и значит, равен 2\angle A
, откуда
\angle HMK=\angle AMH+\angle CMK-180^{\circ}=2(\angle A+\angle C)-180^{\circ}=2\cdot120^{\circ}-180^{\circ}=60^{\circ}.
Следовательно, для любого остроугольного треугольника ABC
с углом 60^{\circ}
при вершине B
, треугольник HMK
— равносторонний.
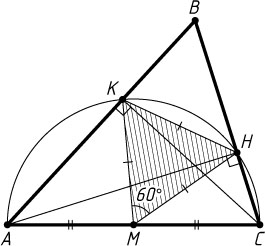
Второй способ. На полуокружности с диаметром AC
и центром M
отметим точки K
и H
так, чтобы дуга KH
составляла 60^{\circ}
и прямые AK
и CH
пересекались вне полукруга. Пусть B
— точка пересечения этих прямых. Тогда K
и H
— основания высот треугольника ABC
(лежащие на его сторонах), треугольник KMH
равносторонний, а если прямая KH
не параллельна диаметру AC
, то треугольник ABC
не будет равносторонним.
Автор: Заславский А. А.
Источник: Турнир городов. — 2007-2008, XXIX, осенний тур, младшие классы, тренировочный вариант

