2362. Точка M
— середина стороны AC
остроугольного треугольника ABC
, AD
— его высота. На отрезке BD
отмечена такая точка E
, что AM=DE
. На отрезке EM
отмечена такая точка F
, что EF=FC
. Докажите, что CF
— биссектриса угла C
треугольника ABC
.
Указание. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.
Решение. Медиана DM
прямоугольного треугольника ADC
равна половине гипотенузы AC
(см. задачу 1109), поэтому DM=\frac{1}{2}AC=MC
. Равнобедренные треугольники EDM
и EFC
имеют общий угол DEF
при основаниях, поэтому \angle EMD=\angle FCE
.
Обозначим \angle FCE=\alpha
. Тогда
\angle DME=\angle CEF=\angle FCE=\alpha.
По теореме о внешнем угле треугольника
\angle CDM=\angle DME+\angle DEM=2\alpha,
а так как треугольник CDM
равнобедренный, то
\angle ACB=\angle MCD=\angle CDM=2\alpha.
Значит, угол ACB
вдвое больше угла FCE
. Следовательно, CF
— биссектриса угла ACB
. Что и требовалось доказать.
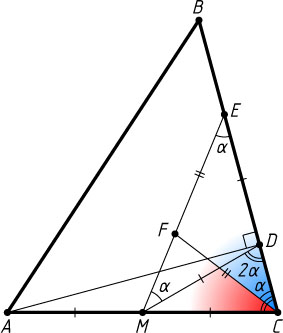
Автор: Пастор А. В.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2011, первый тур, 8 класс
