2415. Точки A_{1}
, B_{1}
и C_{1}
лежат на сторонах соответственно BC
, AC
и AB
треугольника ABC
, причём прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в одной точке. Точки A_{2}
, B_{2}
и C_{2}
соответственно симметричны точкам A_{1}
, B_{1}
и C_{1}
относительно середин сторон, на которых они лежат. Докажите, что прямые AA_{2}
, BB_{2}
и CC_{2}
также пересекаются в одной точке.
Указание. Примените теорему Чевы (см. задачу 1621).
Решение. Прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в одной точке, поэтому по теореме Чевы (см. задачу 1621)
\frac{AB_{1}}{B_{1}C}\cdot\frac{CA_{1}}{A_{1}B}\cdot\frac{BC_{1}}{C_{1}A}=1,
а так как
AB_{2}=CB_{1},~B_{2}C=AB_{1},~CA_{2}=A_{1}B,~BA_{2}=CA_{1},
BC_{2}=AC_{1},~AB_{2}=CB_{1},
то
\frac{AB_{2}}{B_{2}C}\cdot\frac{CA_{2}}{A_{2}B}\cdot\frac{BC_{2}}{C_{2}A}=
=\frac{AB_{1}}{B_{1}C}\cdot\frac{CA_{1}}{A_{1}B}\cdot\frac{BC_{1}}{C_{1}A}=1.
Следовательно, по теореме Чевы прямые AA_{2}
, BB_{2}
и CC_{2}
пересекаются в одной точке.
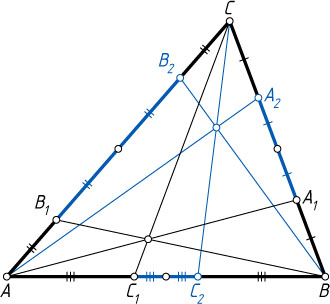
Примечание. Точки A_{2}
, B_{2}
, C_{2}
называются изотомическими точками сторон треугольника, а прямые AA_{2}
, BB_{2}
, CC_{2}
— изотомическими прямыми треугольника. Точка пересечения прямых AA_{1}
, BB_{1}
, CC_{1}
и точка пересечения прямых AA_{2}
, BB_{2}
и CC_{2}
называются изотомически сопряжёнными.
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — с. 132
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 227, с. 188
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 68
