2448. Отрезок постоянной длины движется по плоскости так, что его концы скользят по сторонам прямого угла. По какой траектории движется середина этого отрезка?
Ответ. Четверть окружности.
Указание. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы (см. задачу 1109).
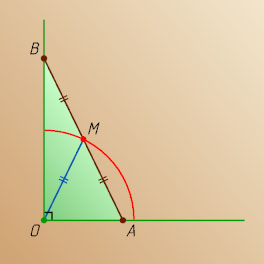
Решение. Пусть O
— вершина данного прямого угла, AB
— данный отрезок, M
— его середина. Тогда OM
— медиана треугольника, проведённая из вершины прямого угла, поэтому OM=\frac{1}{2}AB
(см. задачу 1109). Следовательно, точка M
лежит на окружности с центром в точке O
и радиусом, равным половине данного отрезка.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 7.11, с. 185
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 7.11, с. 184
