2450. На окружности фиксированы точки A
и B
, а точка C
перемещается по этой окружности. Найдите множество точек пересечения биссектрис треугольников ABC
.
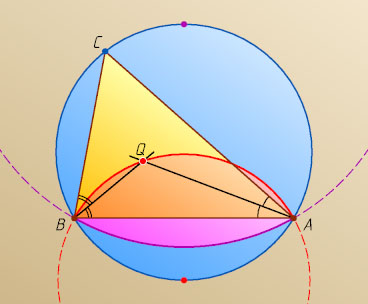
Ответ. Две дуги окружностей.
Указание. Если Q
— точка пересечения биссектрис треугольника ABC
, то \angle AQB=90^{\circ}+\frac{1}{2}\angle C
.
Решение. Пусть Q
— точка пересечения биссектрис треугольника ABC
, а дуги AB
данной окружности равны 2\gamma
и 360^{\circ}-2\gamma
. Если точка C
лежит на дуге, равной 360^{\circ}-2\gamma
, то
\angle AQB=90^{\circ}+\frac{1}{2}\angle C=90^{\circ}+\frac{1}{2}\gamma.
(см. задачу 1101). При этом точки C
и Q
лежат по одну сторону от прямой AB
. Геометрическое место таких точек Q
есть дуга окружности с хордой AB
, вмещающая угол 90^{\circ}+\frac{1}{2}\gamma
.
Аналогично, если точка C
лежит на дуге, равной 2\gamma
, то геометрическое место точек Q
есть дуга окружности с хордой AB
, вмещающая угол
90^{\circ}+\frac{1}{2}(180^{\circ}-\gamma)=180^{\circ}-\frac{1}{2}\gamma.
Таким образом, искомое геометрическое место есть фигура, состоящая из двух указанных дуг.
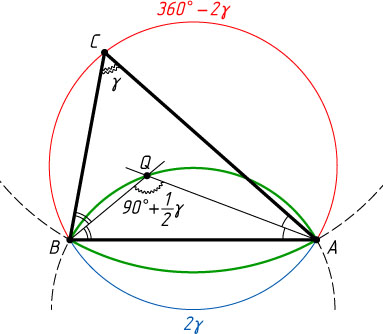
Примечание. Заметим, что из задачи 788 следует, что центры окружностей, из дуг которых состоит искомое ГМТ, лежат на исходной окружности.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 7.18(б), с. 186
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 7.19(б), с. 185

