2472. Диагонали вписанного четырёхугольника ABCD
пересекаются в точке E
; точки K
и M
— середины сторон AB
и CD
; L
и N
— проекции точки E
на стороны BC
и AD
. Докажите, что прямые KM
и LN
перпендикулярны.
Указание. Пусть X
и Y
— середины отрезков соответственно AE
и BE
. Тогда треугольники NXK
и KYL
равны.
Решение. Пусть X
— середина отрезка AE
, Y
— середина отрезка BE
. Отрезки NX
и LY
— медианы прямоугольных треугольников ANE
и BLE
, проведённые из вершин прямых углов, а KX
и KY
— средние линии треугольника AEB
, поэтому (см. задачу 1109)
NX=\frac{1}{2}AE=KY,~KX=\frac{1}{2}BE=LY.
Кроме того, четырёхугольник KXEY
— параллелограмм, вписанные углы CAD
и CBD
опираются на одну и ту же дугу, а NXE
и LYE
— внешние углы треугольников AXN
и BYL
, поэтому
\angle KXE=\angle KYE,~\angle NXE=2\angle CAD=2\angle CBD=\angle LYE.
Значит,
\angle NXK=\angle NXE+\angle KXE=\angle KYE+\angle LYE=\angle KYL.
Следовательно, треугольники NXK
и KYL
равны по двум сторонам и углу между ними. Поэтому KN=KL
, т. е. точка K
равноудалена от концов отрезка NL
. Аналогично точка M
также равноудалена от концов этого отрезка. Значит, прямая KM
— серединный перпендикуляр к отрезку NL
. Отсюда следует утверждение задачи.
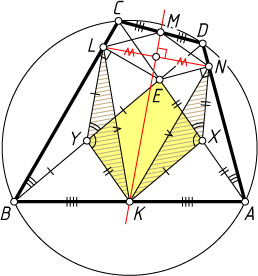
Автор: Кожевников П. А.
Источник: Журнал «Квант». — 2007, № 5, с. 21, М2037
Источник: Задачник «Кванта». — М2037
