2524. С помощью циркуля и линейки восстановите выпуклый четырёхугольник по четырём точкам — проекциям точки пересечения его диагоналей на стороны.
Указание. Пусть M
, N
, K
и L
— данные точки, Q
— точка пересечения диагоналей искомого четырёхугольника. Выразите углы LQN
и MQK
через углы четырёхугольника MNKL
.
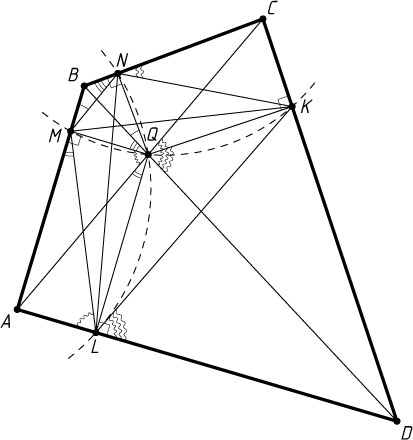
Решение. Предположим, что нужный четырёхугольник ABCD
построен. Пусть M
, N
, K
, L
— проекции точки Q
пересечения диагоналей AC
и BD
на стороны AB
, BC
, CD
, AD
соответственно. Будем считать для определённости, что луч AB
пересекается с лучом DC
, а луч DA
— с лучом CB
. Обозначим углы при вершинах четырёхугольника MNKL
через \varphi_{1}
, \varphi_{2}
, \varphi_{3}
, \varphi_{4}
соответственно,
\angle BQN=\alpha_{1},~\angle AQL=\alpha_{2},~\angle BQM=\alpha_{3},
\angle AQM=\alpha_{4},~\angle CQK=\alpha_{5},~\angle DQK=\alpha_{6}.
Пользуясь тем, что четырёхугольники QMAL
, QNBM
, QKCN
и QLDK
вписанные, получим:
\alpha_{1}+\alpha_{2}+\varphi_{1}=180^{\circ},
\alpha_{1}+\alpha_{2}=180^{\circ}-\varphi_{1},
\alpha_{3}+\alpha_{4}=\alpha_{5}+\alpha_{6},
\alpha_{3}+\alpha_{5}=180^{\circ}-\varphi_{2},
\alpha_{4}+\alpha_{6}=180^{\circ}-\varphi_{4},~\alpha_{3}+\alpha_{4}+\alpha_{5}+\alpha_{6}=360^{\circ}-\varphi_{2}-\varphi_{4},
2(\alpha_{3}+\alpha_{4})=360^{\circ}-\varphi_{2}-\varphi_{4},~\alpha_{3}+\alpha_{4}=180^{\circ}-\frac{1}{2}(\varphi_{2}+\varphi_{4}).
Поэтому
\angle NQL=\alpha_{1}+\alpha_{2}+\alpha_{3}+\alpha_{4}=180^{\circ}-\varphi_{1}+180^{\circ}-\frac{1}{2}(\varphi_{2}+\varphi_{4})=360^{\circ}-\varphi_{1}-\frac{1}{2}(\varphi_{2}+\varphi_{4}).
Аналогично
\angle MQK=360^{\circ}-\varphi_{2}-\frac{1}{2}(\varphi_{1}+\varphi_{3}).
Поэтому данные отрезки LN
и MK
видны из точки Q
под известными углами. Следовательно, точка Q
может быть найдена, как точка пересечения двух соответствующих геометрических мест точек — дуг окружностей, построенных на отрезках LN
и MK
как на хордах, и вмещающих найденные углы (см. задачу 2889). Остаётся провести через данные точки M
, N
, K
и L
перпендикуляры к отрезкам QM
, QN
, QK
и QL
соответственно.
Источник: Петерсен Ю. Методы и теории для решения геометрических задач на построение, приложенные более чем к 400 задачам. — М.: Типография Э. Лисснера и Ю. Романа, 1892. — № 102, с. 20
