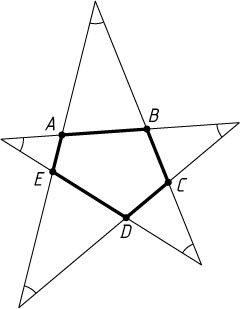
2578. Замкнутая пятизвенная ломаная образует равноугольную звезду (см. рис.). Чему равен периметр внутреннего пятиугольника ABCDE
, если длина исходной ломаной равна 1?
Ответ. \frac{\cos72^{\circ}}{1+\cos72^{\circ}}=\sqrt{5}-2
.
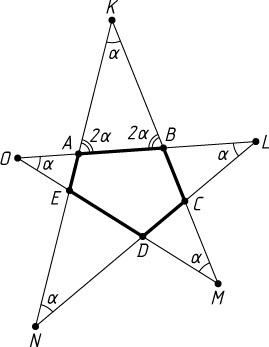
Решение. Пусть K
, L
, M
, N
и O
— вершины звезды, лежащие против сторон соответственно AB
, BC
, CD
, DE
и EA
внутреннего пятиугольника ABCDE
. Обозначим через \alpha
равные углы при вершинах звезды. По теореме о внешнем угле треугольника
\angle KBA=\angle KBO=\angle O+\angle M=2\alpha,
\angle BAK=\angle LAK=\angle L+\angle N=2\alpha.
Тогда \alpha=\angle K=180^{\circ}-4\alpha
, откуда находим, что \alpha=\frac{180^{\circ}}{5}=36^{\circ}
.
Таким образом, треугольники AKB
, BLC
, CMD
, DNE
и AOE
— равнобедренные, а их углы равны 36^{\circ}
, 72^{\circ}
, 72^{\circ}
. Тогда
AB=2KA\cos72^{\circ}=(KA+KB)\cos72^{\circ},
BC=2LB\cos72^{\circ}=(LB+LC)\cos72^{\circ},
CD=2MC\cos72^{\circ}=(MC+MD)\cos72^{\circ},
DE=2ND\cos72^{\circ}=(ND+NE)\cos72^{\circ},
AE=2OE\cos72^{\circ}=(OE+OA)\cos72^{\circ}.
Сложив эти равенства, получим, что
AB+BC+CD+DE+EA=(KA+KB+LB+LC+MC+MD+ND+NE+OE+OA)\cos72^{\circ}=
=(1-AB-BC-CD-DE-EA)\cos72^{\circ},
следовательно,
AB+BC+CD+DE+EA=\frac{\cos72^{\circ}}{1+\cos72^{\circ}}.
Примечание. Зная, что \sin18^{\circ}=\frac{\sqrt{5}-1}{4}
(см. задачу 1494), последнее выражение можно упростить:
\frac{\cos72^{\circ}}{1+\cos72^{\circ}}=\frac{\sin18^{\circ}}{1+\sin18^{\circ}}=\frac{\frac{\sqrt{5}-1}{4}}{1+\frac{\sqrt{5}-1}{4}}=\frac{\sqrt{5}-1}{3+\sqrt{5}}=\sqrt{5}-2.
Автор: Нецветаев Н. Ю.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1989, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 89.30

