1494. Найдите синус и косинус 18^{\circ}
.
Ответ. \frac{\sqrt{5}-1}{4}
; \sqrt{\frac{5+\sqrt{5}}{8}}
.
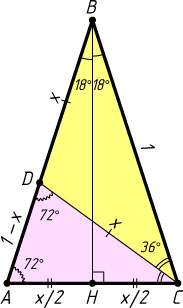
Решение. Первый способ. Рассмотрим равнобедренный треугольник ABC
с углами \angle ABC=36^{\circ}
, \angle BAC=\angle ACB=72^{\circ}
. Пусть AB=BC=1
, AC=x
. Высота BH
этого треугольника является медианой и биссектрисой. Пусть CD
— биссектриса треугольника ABC
. Тогда
\angle BCD=\angle ACD=36^{\circ},~~\angle ADC=72^{\circ},
значит, треугольники ACD
и BCD
равнобедренные. Поэтому
AC=CD=BD=x,~AD=BD=1-x.
По свойству биссектрисы треугольника \frac{BD}{AD}=\frac{BC}{AC}
(см. задачу 1509), или \frac{x}{1-x}=\frac{1}{x}
. Значит, x^{2}+x-1=0
. Число x=\frac{\sqrt{5}-1}{2}
— положительный корень этого уравнения. Следовательно,
\sin18^{\circ}=\sin\angle ABH=\frac{AH}{AB}=\frac{\frac{x}{2}}{1}=\frac{x}{2}=\frac{\sqrt{5}-1}{4}.
Применяя формулу \sin^{2}\alpha+\cos^{2}\alpha=1
, находим, что
\cos18^{\circ}=\sqrt{1-\sin^{2}18^{\circ}}=\sqrt{1-\left(\frac{\sqrt{5}-1}{4}\right)^{2}}=\sqrt{\frac{16-(\sqrt{5}-1)^{2}}{16}}=
=\sqrt{\frac{10+2\sqrt{5}}{16}}=\sqrt{\frac{5+\sqrt{5}}{8}}.
Второй способ. Поскольку
\sin54^{\circ}-\sin18^{\circ}=\frac{2\cos18^{\circ}(\sin54^{\circ}-\sin18^{\circ})}{2\cos18^{\circ}}=
=\frac{2\sin54^{\circ}\cos18^{\circ}-2\sin18^{\circ}\cos18^{\circ}}{2\cos18^{\circ}}=\frac{\sin72^{\circ}+\sin36^{\circ}-\sin36^{\circ}}{2\cos18^{\circ}}=
=\frac{\sin72^{\circ}}{2\cos18^{\circ}}=\frac{\cos18^{\circ}}{2\cos18^{\circ}}=\frac{1}{2}
и
\sin18^{\circ}\sin54^{\circ}=\frac{2\cos18^{\circ}\sin54^{\circ}\sin18^{\circ}}{2\cos18^{\circ}}=\frac{\sin36^{\circ}\sin54^{\circ}}{2\cos18^{\circ}}=
=\frac{\frac{1}{2}(\cos(54^{\circ}-36^{\circ})-\cos(54^{\circ}+36^{\circ}))}{2\cos18^{\circ}}=\frac{\frac{1}{2}(\cos18-\cos90^{\circ})}{2\cos18^{\circ}}=\frac{\cos18^{\circ}}{4\cos18^{\circ}}=\frac{1}{4},
то, обозначив \sin18^{\circ}=t
и \sin54^{\circ}=z
, получим систему
\syst{z-t=\frac{1}{2}\\tz=\frac{1}{4},\\}
из которой находим, что
\sin18^{\circ}=t=\frac{\sqrt{5}-1}{4}.
Тогда
\cos18^{\circ}=\sqrt{1-\sin^{2}18^{\circ}}=\sqrt{1-\left(\frac{\sqrt{5}-1}{4}\right)^{2}}=\sqrt{\frac{5+\sqrt{5}}{8}}.
Третий способ. Рассмотрим правильный пятиугольник ABCDE
с центром O
, OA=1
. Поместим начало координат в точку O
, направим ось Ox
по лучу OA
, а ось Oy
— по лучу, перпендикулярному OA
и содержащемуся с вершиной B
в одной полуплоскости относительно прямой OA
. Тогда абсциссы векторов \overrightarrow{OA}
, \overrightarrow{OB}
, \overrightarrow{OC}
, \overrightarrow{OD}
и \overrightarrow{OE}
равны
1,~\cos72^{\circ}=\sin18^{\circ},~\cos144^{\circ}=-\cos36^{\circ},~\cos216^{\circ}=-\cos36^{\circ},~\cos288^{\circ}=\sin18^{\circ},
в так как
\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}=\overrightarrow{0}
(см. задачу 4522), то
1+\sin18^{\circ}-\cos36^{\circ}-\cos36^{\circ}+\sin18^{\circ}=1+2\sin18^{\circ}-2\cos36^{\circ}=
=1+2\sin18^{\circ}-2(1-2\sin^{2}18^{\circ})=4\sin^{2}18^{\circ}+2\sin18^{\circ}-1=0.
Отсюда находим, что \sin18^{\circ}=\frac{\sqrt{5}-1}{4}
. Тогда
\cos18^{\circ}=\sqrt{1-\sin^{2}18^{\circ}}=\sqrt{1-\left(\frac{\sqrt{5}-1}{4}\right)^{2}}=\sqrt{\frac{5+\sqrt{5}}{8}}.
Четвёртый способ. Рассмотрим равнобедренный треугольник ABC
с углом 108^{\circ}
при вершине A
. Пусть r
и R
— радиусы его соответственно вписанной и описанной окружностей. Их центры соответственно I
и O
симметричны относительно прямой BC
(см. задачу 1702), поэтому IO=2r
. Поскольку CI
— биссектриса угла ACB
, равного 36^{\circ}
, то
\sin18^{\circ}=\frac{IK}{CI}=\frac{r}{R},
где K
— середина основания BC
.
По формуле Эйлера (см. задачу 126) IO^{2}=R^{2}-2rR
. Значит,
4r^{2}=R^{2}-2rR~\Leftrightarrow~4\left(\frac{r}{R}\right)^{2}+2\left(\frac{r}{R}\right)-1=0~\Leftrightarrow~4\sin^{2}18^{\circ}+2\sin18^{\circ}-1=0.
Отсюда находим, что \sin18^{\circ}=\frac{\sqrt{5}-1}{4}
(второй корень отрицательный). Тогда
\cos18^{\circ}=\sqrt{1-\sin^{2}18^{\circ}}=\sqrt{1-\left(\frac{\sqrt{5}-1}{4}\right)^{2}}=\sqrt{\frac{5+\sqrt{5}}{8}}.
Примечание. См. также Crux Mathematicorum, 1986, N7, с.168
