2598. В окружность вписан четырёхугольник ABCD
. Прямые AB
и CD
пересекаются в точке M
, а прямые BC
и AD
— в точке N
. Известно, что BM=DN
. Докажите, что CM=CN
.
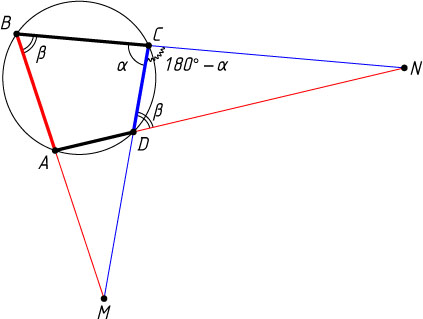
Решение. Первый способ. Обозначим \angle BCM=\alpha
, \angle CBM=\beta
(рис. 1). Тогда
\angle DCN=180^{\circ}-\angle BCM=180^{\circ}-\alpha,
\angle CDN=180^{\circ}-\angle ADC=180^{\circ}-(180^{\circ}-\angle ABC)=\angle ABC=\beta.
Применяя теорему синусов к треугольникам BCM
и CDN
получим, что
\frac{BM}{\sin\alpha}=\frac{CM}{\sin\beta},~\frac{CN}{\sin\beta}=\frac{DN}{\sin(180^{\circ}-\alpha)}=\frac{DN}{\sin\alpha},
а так как BM=DN
, то \frac{CM}{\sin\beta}=\frac{CN}{\sin\beta}
. Следовательно, CM=CN
.
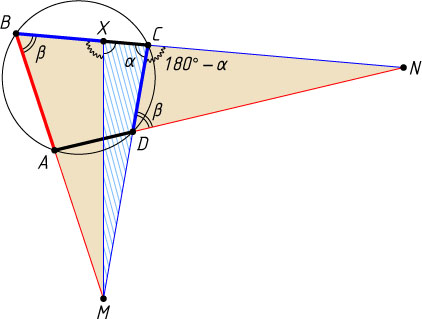
Второй способ. (Решение С.Коротких.) Обозначим \angle BCM=\alpha
, \angle CBM=\beta
. На луче BN
отложим отрезок BX=CD
(рис. 2). Тогда
\angle CDN=180^{\circ}-\angle ADC=180^{\circ}-(180^{\circ}-\beta)=\beta.
Значит, треугольник XBM
равен треугольнику CDN
по двум сторонам и углу между ними. Поэтому MX=CN
и
\angle BXM=\angle DCN=180^{\circ}-\alpha,~\angle CXM=180^{\circ}-\angle BXM=\alpha=\angle XCM.
Следовательно, треугольник CMX
равнобедренный, MX=CM
, а так как MX=CN
, то CM=CN
. Что и требовалось доказать.
Примечание. Точка P
, полученная в этом способе решения, есть точка Микеля для прямых NA
, NB
, MA
и MD
. Через эту точку проходят также окружности, описанные около треугольников ANB
и AMD
(см. задачу 995).
Автор: Назаров Ф. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1993, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 93.22
Источник: Мерзляк А. Г., Поляков В. М. Геометрия. 9 класс. Углублённый уровень. — М.: Вентана-Граф, 2020. — № 3.42, с. 29
Источник: Московская математическая регата. — 2014-2015, второй тур, № 2, 11 класс

