2599. Внутри треугольника ABC
расположена окружность, которая касается его сторон AB
и BC
, а также проходит через точку P
— центр вписанной окружности треугольника ABC
. Через точки A
, P
и C
проведена другая окружность. Докажите, что эти окружности касаются друг друга.
Решение. Первый способ. Заметим, что P
— точка пересечения биссектрис треугольника ABC
, значит, точки B
, P
и центр первой окружности лежат на одной прямой. Поэтому достаточно доказать, что центр окружности, проходящей через точки A
, P
и C
, также лежит на это прямой, т. е. на биссектрисе угла ABC
, так как тогда общая точка P
двух окружностей лежит на их линии центров, а это и означает, что P
— точка касания окружностей.
Обозначим углы треугольника ABC
через \alpha
, \beta
и \gamma
соответственно. Пусть серединный перпендикуляр к отрезку AP
пересекается с прямой BP
в точке O
. Тогда
\angle AOP=180^{\circ}-2\angle APO=180^{\circ}-2(\angle ABP+\angle BAP)=180^{\circ}-2\left(\frac{\beta}{2}+\frac{\alpha}{2}\right)=180^{\circ}-\alpha-\beta=\gamma,
а так как \angle ACP=\frac{\gamma}{2}
, то \angle AOP=2\angle ACP
. При этом OA=OP
, так как точка O
лежит на серединном перпендикуляре к отрезку AP
, значит, окружность с центром O
и радиусом OP
проходит через точку C
(см. задачу 2900). Следовательно, это окружность, описанная около треугольника APC
, а её центр O
лежит на прямой BP
. Что и требовалось доказать.
Второй способ. Докажем следующее утверждение. Если O
— точка пересечения биссектрисы угла B
треугольника ABC
с описанной окружностью этого треугольника, а P
— центр вписанной окружности треугольника, то OA=OP=OC
(см. задачу 788).
Обозначим углы \angle BAC=\alpha
, \angle ABC=\beta
. Тогда по теореме о внешнем угле треугольника
\angle APO=\angle BAP+\angle ABP=\frac{\alpha}{2}+\frac{\beta}{2}.
В то же время,
\angle OAP=\angle CAP+\angle CAO=\angle CAP+\angle CBO=\frac{\alpha}{2}+\frac{\beta}{2},
значит, \angle APO=\angle OAP
. Следовательно, OA=OP
.
Аналогично докажем, что OC=OP
.
Из доказанного утверждения следует, что центр O
окружности, описанной около треугольника APC
, лежит на биссектрисе угла ABC
, а так как на этой же биссектрисе лежит и точка P
, и центр окружности, о которой говорится в условии задачи, то P
— точка касания этих окружностей. Что и требовалось доказать.
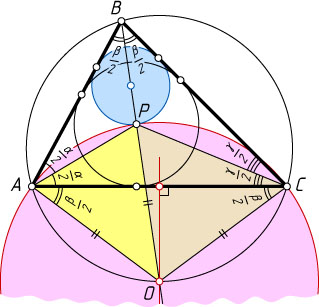
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1993, 10 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 93.29
