2622. Высоты BB_{1}
и CC_{1}
остроугольного треугольника ABC
пересекаются в точке H
, причём CH=C_{1}H
и BH=2B_{1}H
. Найдите угол BAC
.
Ответ. 45^{\circ}
.
Указание. Пусть M
— середина BH
. Тогда четырёхугольник CB_{1}C_{1}M
— параллелограмм.
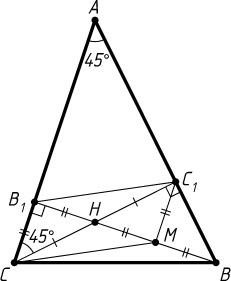
Решение. Первый способ. Пусть M
— середина BH
(рис. 1). Поскольку диагонали CC_{1}
и MB_{1}
четырёхугольника CB_{1}C_{1}M
точкой H
пересечения делятся пополам, то CB_{1}C_{1}M
— параллелограмм. Поэтому CB_{1}\parallel C_{1}M
и CB_{1}=C_{1}M
. С другой стороны, C_{1}M
— медиана прямоугольного треугольника BC_{1}H
, проведённая из вершины прямого угла C_{1}
, поэтому (см. задачу 1109)
C_{1}M=\frac{1}{2}BH=MH=B_{1}H.
Значит, катеты CB_{1}
и B_{1}H
прямоугольного треугольника CB_{1}H
равны между собой. Следовательно,
\angle ACC_{1}=45^{\circ},~\angle A=45^{\circ}.
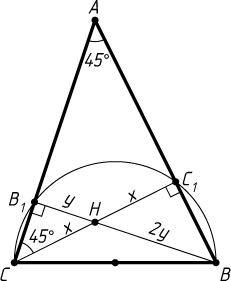
Второй способ. Точки B_{1}
и C_{1}
лежат на окружности с диаметром BC
(рис. 2). Обозначим
CH=C_{1}H=x,~B_{1}H=y,~BH=2y.
По теореме о произведениях отрезков пересекающихся хорд CH\cdot C_{1}H=BH\cdot B_{1}H
, или x^{2}=2y^{2}
, откуда x=y\sqrt{2}
. Значит, в прямоугольном треугольнике CB_{1}H
угол B_{1}CH
равен 45^{\circ}
. Следовательно,
\angle A=90^{\circ}-\angle B_{1}CH=45^{\circ}.
Источник: Соросовская олимпиада. — 1997-1998, IV, 2-й тур, 9 класс

