2651. Стороны треугольника равны 11, 13 и 12. Найдите медиану, проведённую к большей стороне.
Ответ. \frac{19}{2}
.
Указание. Воспользуйтесь теоремой о сумме квадратов диагоналей параллелограмма или формулой для медианы треугольника.
Решение. Пусть AM
— медиана треугольника ABC
, в котором AB=12
, AC=11
, BC=13
. На продолжении медианы AM
за точку M
отложим отрезок MK
, равный AM
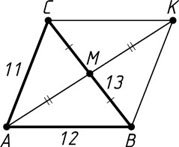
. Тогда ABKC
— параллелограмм. По теореме о сумме квадратов диагоналей параллелограмма (см. задачу 4011)
AK^{2}+BC^{2}=2AB^{2}+2AC^{2},
откуда
AK^{2}=2AB^{2}+2AC^{2}-BC^{2}=288+242-169=361=19^{2}.
Следовательно, AM=\frac{1}{2}AK=\frac{19}{2}
.
Источник: Вступительный экзамен в МИЭТ. — 1977
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 4, с. 184
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 2.4, с. 17
