2652. В треугольнике две стороны равны 11 и 23, а медиана, проведённая к третьей, равна 10. Найдите третью сторону.
Ответ. 30.
Указание. Воспользуйтесь теоремой о сумме квадратов диагоналей параллелограмма или формулой для медианы треугольника.
Решение. Первый способ. Пусть CM
— медиана треугольника ABC
, в котором AC=11
, BC=23
, CM=10
. Тогда (см. задачу 4014)
CM^{2}=\frac{1}{4}(2AC^{2}+2BC^{2}-AB^{2}),~\mbox{или}~100=\frac{1}{4}(2\cdot121+2\cdot529-AB^{2}).
Отсюда находим, что AB^{2}=900
.
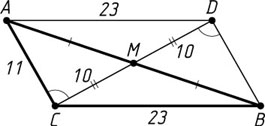
Второй способ. Пусть CM
— медиана треугольника ABC
, в котором AC=11
, BC=23
, CM=10
. На продолжении медианы CM
за точку M
отложим отрезок MD
, равный CM
. Тогда ACBD
— параллелограмм, CD=20
, DB=11
. По теореме косинусов найдём \cos\angle CDB
из треугольника CDB
, а затем — отрезок BM
из треугольника MDB
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 3, с. 92
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 2.5, с. 17
