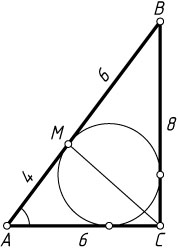
2661. Окружность, вписанная в прямоугольный треугольник с катетами 6 и 8, касается гипотенузы в точке M
. Найдите расстояние от точки M
до вершины прямого угла.
Ответ. 2\sqrt{\frac{29}{5}}
.
Указание. Пусть окружность, вписанная в треугольник ABC
, касается стороны AB
в точке M
. Тогда AM=p-BC
, где p
— полупериметр треугольника ABC
(см. задачу 219).
Решение. Пусть окружность, вписанная в прямоугольный треугольник ABC
, касается гипотенузы AB
в точке M
. Если AC=6
и BC=8
, то
AB=\sqrt{AC^{2}+BC^{2}}=10,~\cos\angle A=\frac{AC}{AB}=\frac{3}{5}.
Пусть p
— полупериметр треугольника ABC
. Тогда
AM=p-BC=12-8=4
(см. задачу 219). По теореме косинусов из треугольника AMC
находим, что
CM^{2}=AC^{2}+AM^{2}-2AC\cdot AM\cos\angle A=36+16-2\cdot6\cdot4\cdot\frac{3}{5}=\frac{116}{5}.
Следовательно,
CM=\sqrt{\frac{116}{5}}=2\sqrt{\frac{29}{5}}.