2675. Пользуясь только циркулем, разделите пополам дугу окружности с данным центром.
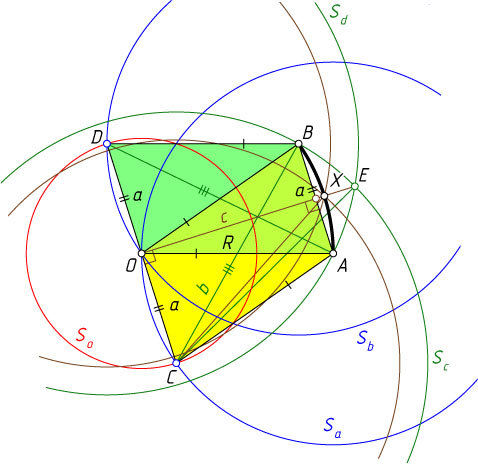
Решение. Пусть O
— центр окружности радиуса R
, AB
— дуга окружности. Обозначим AB=a
. С центрами в точках A
и B
построим окружности S_{a}
и S_{b}
радиуса R
, с центром в точке O
— окружность S_{o}
радиуса a
.
Пусть C
и D
— точки пересечения окружности S_{o}
с окружностями S_{a}
и S_{b}
соответственно. Тогда OC=AB=OD=a
и AC=AO=OB=BD=R
. Противоположные стороны каждого из четырёхугольников ABOC
и ABDO
попарно равны, значит, ABOC
и ABDO
— параллелограммы. Поэтому OC\parallel AB\parallel OD
. Следовательно, точки C
, O
и D
лежат на одной прямой.
Обозначим AD=BC=b
. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон (см. задачу 4011), поэтому OA^{2}+BC^{2}=2AB^{2}+2OC^{2}
, или R^{2}+b^{2}=2a^{2}+2R^{2}
, откуда находим, что b^{2}=2a^{2}+R^{2}
.
С центрами в точках C
и D
построим окружности S_{c}
и S_{d}
радиуса b
. Пусть E
— точка пересечения этих окружностей. Поскольку CE=DE=b
, прямая OE
— серединный перпендикуляр к отрезку CD
, а так как AB\parallel CD
и OA=OB
, то OE
— серединный перпендикуляр и к отрезку AB
.
Обозначим OE=c
. Из прямоугольного треугольника COE
находим, что
c^{2}=OE^{2}=CE^{2}-OC^{2}=b^{2}-a^{2}=2a^{2}+R^{2}-a^{2}=a^{2}+R^{2}.
С центрами в точках C
и D
строим окружности радиуса c
. Пусть X
— точка их пересечения, лежащая по ту же сторону от прямой CD
, что и точка E
. Докажем, что X
— искомая середина дуги AB
.
Действительно, поскольку CX=DX
— точка X
лежит на серединном перпендикуляре к отрезку CD
, т. е. на прямой OE
. Кроме того, из прямоугольного треугольника XOC
находим, что
OX^{2}=CX^{2}-OC^{2}=c^{2}-a^{2}=a^{2}+R^{2}-a^{2}=R^{2}.
Что и требовалось доказать.
Таким образом, точка X
равноудалена от концов отрезка AB
и лежит на данной дуге AB
. Следовательно, X
— середина этой дуги.
Заметим, что вторая точка пересечения окружностей радиуса c
с центрами C
и D
— середина дуги, дополнительной к дуге AB
.
Источник: Курант Р., Роббинс Г. Что такое математика?. — 2-е изд. — М.: Просвещение, 1976. — с. 178
Источник: Костовский А. Н. Геометрические построения одним циркулем на плоскости и одним лишь сферографом в пространстве. — (Популярные лекции по математике. Вып. 29). — 3-е изд., перераб. и доп. — М.: Наука, 1989. — с. 11
