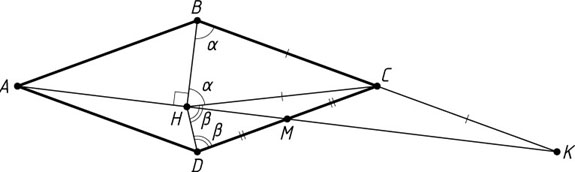
2736. Острый угол при вершине A
ромба ABCD
равен 40^{\circ}
. Через вершину A
и середину M
стороны CD
проведена прямая, на которую опущен перпендикуляр BH
из вершины B
. Найдите угол AHD
.
Ответ. 110^{\circ}
.
Указание. Продолжите сторону BC
до пересечения с прямой AM
в точке K
. Тогда HC
— медиана прямоугольного треугольника BHK
, проведённая из вершины прямого угла.
Решение. Продолжим сторону BC
до пересечения с прямой AM
в точке K
. Тогда CK=AD=BC
, т. е. HC
— медиана прямоугольного треугольника BHK
, проведённая из вершины прямого угла, поэтому HC=BC=CD
(см. задачу 1109). Обозначим через \alpha
и \beta
углы при основаниях BH
и DH
равнобедренных треугольников BCH
и CDH
соответственно. Тогда
\angle BHD=\angle BHC+\angle CHD=\alpha+\beta=90^{\circ}-\frac{1}{2}\angle BCH+90^{\circ}-\frac{1}{2}\angle DCH=
=180^{\circ}-\frac{1}{2}(\angle BCH+\angle DCH)=180^{\circ}-\frac{1}{2}\angle BCD=180^{\circ}-20^{\circ}=160^{\circ}.
Следовательно,
\angle AHD=360^{\circ}-\angle AHB-\angle BHD=360^{\circ}-90^{\circ}-160^{\circ}=110^{\circ}.
Источник: Московская математическая олимпиада. — 1997, LX, 8 класс
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.26, с. 12
Источник: Фёдоров Р. М. и др. Московские математические олимпиады. 1993—2005 / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. — № 5, с. 33
Источник: Международная олимпиада «Интеллектуальный марафон». — 1998, VIII, письменный индивидуальный командный тур, задача 6
Источник: Журнал «Квант». — 1999, № 6, с. 40, задача 7
