2766. В прямоугольном треугольнике отношение радиуса вписанной окружности к радиусу описанной окружности равно \frac{2}{5}
. Найдите острые углы треугольника.
Ответ. \frac{\pi}{4}\pm\arccos\frac{7\sqrt{2}}{10}
, или \arctg\frac{3}{4}
, \arcctg\frac{3}{4}
.
Указание. Радиус окружности, вписанной в прямоугольный треугольник с катетами a
, b
и гипотенузой c
, равен \frac{a+b-c}{2}
(см. задачу 217).
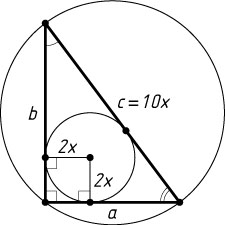
Решение. Первый способ. Пусть радиус вписанной окружности прямоугольного треугольника с катетами a
, b
и гипотенузой c
равен 2x
, а радиус описанной окружности — 5x
. Тогда c=10x
. Поэтому a^{2}+b^{2}=100x^{2}
.
Поскольку радиус окружности, вписанной в прямоугольный треугольник равен \frac{a+b-c}{2}
(см. задачу 217), то имеем ещё одно уравнение
a+b=14x.
Из полученной системы уравнений, находим, что
a=8x,~b=6x,~\mbox{или}~a=6x,~b=8x.
Следовательно, тангенсы острых углов треугольника равны \frac{3}{4}
и \frac{4}{3}
.
Второй способ. Пусть катеты данного прямоугольного треугольника равны a
и b
, гипотенуза равна c
, а угол треугольника, противолежащий катету a
, равен \alpha
(будем считать, что \alpha\leqslant\frac{\pi}{4}
). Тогда радиус описанной окружности равен \frac{c}{2}
,
\sin\alpha=\frac{a}{c},~\cos\alpha=\frac{b}{c},
а так как радиус окружности, вписанной в прямоугольный треугольник равен \frac{a+b-c}{2}
, то
\frac{\frac{a+b-c}{2}}{\frac{c}{2}}=\frac{2}{5}~\Rightarrow~\frac{a}{c}+\frac{b}{c}=\frac{7}{5}~\Rightarrow
\Rightarrow~\sin\alpha+\cos\alpha=\frac{7}{5}~\Rightarrow~\cos\left(\alpha-\frac{\pi}{4}\right)=\frac{7}{5\sqrt{2}},
откуда находим, что
\alpha=\frac{\pi}{4}+\arccos\frac{7\sqrt{2}}{10}.
Тогда второй острый угол равен
\frac{\pi}{2}-\alpha=\frac{\pi}{4}-\arccos\frac{7\sqrt{2}}{10}.
Источник: Вступительный экзамен в МФТИ. — 1947, билет 5, № 1
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 47-5-1, с. 7
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 20, с. 170
Источник: Вступительный экзамен на физический факультет МГУ. — 1994 (предварительный экзамен), № 4, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.12, с. 87
