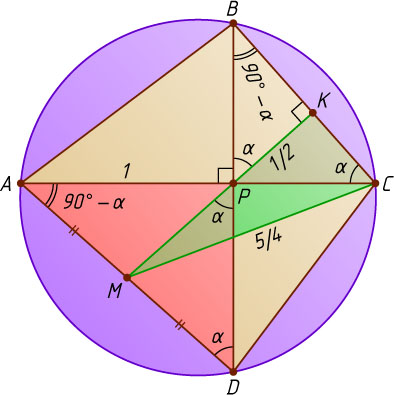
2777. В четырёхугольнике ABCD
диагонали AC
и BD
перпендикулярны и пересекаются в точке P
. Длина отрезка, соединяющего вершину C
с точкой M
, являющейся серединой отрезка AD
, равна \frac{5}{4}
. Расстояние от точки P
до отрезка BC
равно \frac{1}{2}
и AP=1
. Найдите AD
, если известно, что вокруг четырёхугольника ABCD
можно описать окружность.
Ответ. \frac{3\sqrt{6}-2}{4}
.
Указание. Докажите, что PM\perp BC
, обозначьте \angle ADB=\angle ACB=\alpha
и составьте тригонометрическое уравнение относительно \alpha
.
Решение. Пусть прямая MP
пересекает отрезок BC
в точке K
. Обозначим \angle ADB=\angle ACB=\alpha
. Поскольку PM
— медиана прямоугольного треугольника APD
, проведённая из вершины прямого угла, то (см. задачу 1109)
PM=MA=MD,~\angle BPK=\angle DPM=\angle ADB=\alpha,
а так как \angle CBP=90^{\circ}-\alpha
, то
\angle BKP=180^{\circ}-\alpha-(90^{\circ}-\alpha)=90^{\circ},
т. е. PK\perp BC
. Значит, PK=\frac{1}{2}
.
Из прямоугольных треугольников APD
и CKP
находим, что
MP=\frac{1}{2}AD=\frac{1}{2}\cdot\frac{AP}{\sin\alpha}=\frac{1}{2\sin\alpha},~CK=KP\ctg\alpha=\frac{1}{2}\ctg\alpha,
поэтому
MK=MP+KP=\frac{1}{2\sin\alpha}+\frac{1}{2}.
Применяя теорему Пифагора к прямоугольному треугольнику MKC
, получим уравнение
\left(\frac{1}{2\sin\alpha}+\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\ctg\alpha\right)^{2}=\frac{25}{16},
из которого находим, что \frac{1}{\sin\alpha}=\frac{3\sqrt{6}-2}{4}
. Следовательно,
AD=\frac{AP}{\sin\alpha}=\frac{1}{\sin\alpha}=\frac{3\sqrt{6}-2}{4}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1994 (основной экзамен), № 5, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.14, с. 11
