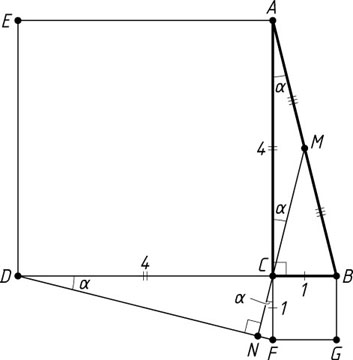
2780. Вне прямоугольного треугольника ABC
на его катетах AC
и BC
построены квадраты ACDE
и BCFG
. Продолжение медианы CM
треугольника ABC
пересекает прямую DF
в точке N
. Найдите отрезок CN
, если катеты равны 1 и 4.
Ответ. \frac{4}{\sqrt{17}}
.
Указание. Докажите, что CN
— высота прямоугольного треугольника CDF
.
Решение. Пусть AC=4
, BC=1
. Обозначим \angle BAC=\alpha
. Прямоугольные треугольники ABC
и DFC
равны по двум катетам, поэтому
DF=AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{17}.
Медиана CM
прямоугольного треугольника ABC
, проведённая к гипотенузе AB
, равна половине гипотенузы (см. задачу 1109), поэтому
\angle NCF=\angle ACM=\angle BAC=\alpha,
\angle CNF=180^{\circ}-\angle NCF-\angle CFN=180^{\circ}-\alpha-(90^{\circ}-\alpha)=90^{\circ},
т. е. CN
— высота прямоугольного треугольника CDF
, проведённая из вершины прямого угла C
. Поскольку CD\cdot CF=DF\cdot CN
(удвоенная площадь треугольника CDF
), то
CN=\frac{CD\cdot CF}{DF}=\frac{4}{\sqrt{17}}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1994, основной экзамен, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 610
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.8, с. 10
