2782. У треугольника известны стороны a=2
, b=3
и площадь S=\frac{3\sqrt{15}}{4}
. Медиана, проведённая к его третьей стороне, меньше её половины. Найдите радиус описанной около треугольника окружности.
Ответ. \frac{8}{\sqrt{15}}
.
Указание. Докажите, что угол, противолежащей третьей стороне, тупой и воспользуйтесь теоремой косинусов и обобщённой теоремой синусов.
Решение. Пусть \alpha
— угол треугольника, противолежащий третьей стороне, равной c
. По формуле площади треугольника
S=\frac{1}{2}ab\sin\alpha,
откуда \sin\alpha=\frac{2S}{ab}=\frac{\sqrt{15}}{4}
.
Поскольку медиана, проведённая к стороне, равной c
, меньше \frac{1}{2}c
, то вершина угла \alpha
данного треугольника лежит внутри окружности, построенной на стороне c
как на диаметре, значит, угол \alpha
— тупой (см. задачу 1772), поэтому
\cos\alpha=-\sqrt{1-\sin^{2}\alpha}=-\frac{1}{4}.
По теореме косинусов
c^{2}=a^{2}+b^{2}-2ab\cos\alpha=4+9+3=16,
поэтому c=4
. Если R
— радиус описанной окружности данного треугольника, то
R=\frac{c}{2\sin\alpha}=\frac{4}{\frac{\sqrt{15}}{2}}=\frac{8}{\sqrt{15}}.
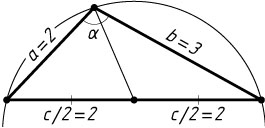
Источник: Вступительный экзамен на геологический факультет МГУ. — 1994 (предварительный экзамен), № 7, вариант 1
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 1.32, с. 13
