2791. На боковой стороне AB
трапеции ABCD
взята такая точка M
, что AM:BM=2:3
. На противоположной стороне CD
взята такая точка N
, что отрезок MN
делит трапецию на части, одна из которых по площади втрое больше другой. Найдите отношение CN:DN
, если BC:AD=1:2
.
Ответ. 3:29
.
Указание. Продолжите боковые стороны трапеции до пересечения в точке P
и воспользуйтесь равенством
S_{\triangle MPN}=\frac{PM}{PA}\cdot\frac{PN}{PD}\cdot S_{\triangle APD}
(см. задачу 3007).
Рассмотрите два случая.
Решение. Пусть продолжения боковых сторон AB
и CD
трапеции пересекаются в точке P
. Тогда BC
— средняя линия треугольника APD
. Поэтому
\frac{PM}{PA}=\frac{8}{10}=\frac{4}{5}.
Обозначим через S
площадь трапеции ABCD
. Тогда площадь треугольника BPC
равна \frac{1}{3}S
.
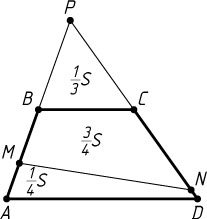
Предположим, что площадь четырёхугольника AMND
в три раза меньше площади четырёхугольника MBCN
. Тогда
S_{\triangle APD}=\frac{4}{3}S,~S_{MBCN}=\frac{3}{4}S,~S_{\triangle MPN}=\frac{1}{3}S+\frac{3}{4}S=\frac{13}{12}S,
а так как
S_{\triangle MPN}=\frac{PM}{PA}\cdot\frac{PN}{PD}S_{\triangle APD}
(см. задачу 3007), то
\frac{13}{12}S=\frac{4}{5}\cdot\frac{PN}{PD}\cdot\frac{4}{3}S,
откуда находим, что \frac{PN}{PD}=\frac{65}{64}\gt1
, т. е. PN\gt PD
, что невозможно, так как точка N
должна принадлежать отрезку CD
.
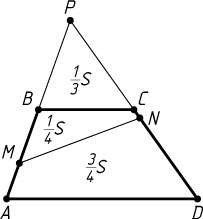
Пусть теперь площадь четырёхугольника MBCN
в три раза меньше площади четырёхугольника AMND
. Тогда
S_{\triangle APD}=\frac{4}{3}S,~S_{MBCN}=\frac{1}{4}S,~S_{\triangle MPN}=\frac{1}{3}S+\frac{1}{4}S=\frac{7}{12}S,
а так как
S_{\triangle MPN}=\frac{PM}{PA}\cdot\frac{PN}{PD}S_{\triangle APD},
то
\frac{7}{12}S=\frac{4}{5}\cdot\frac{PN}{PD}\cdot\frac{4}{3}S,
откуда находим, что \frac{PN}{PD}=\frac{35}{64}
. Следовательно,
\frac{PN}{ND}=\frac{35}{29},~\frac{CN}{ND}=\frac{35-32}{29}=\frac{3}{29}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1995 (предварительный экзамен), № 4, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.37, с. 33

