2792. На боковых сторонах AD
и BC
трапеции ABCD
взяты точки P
и Q
соответственно, причём AP:PD=3:2
. Отрезок PQ
разбивает трапецию на части, одна из которых по площади вдвое больше другой. Найдите отношение CQ:QB
, если AB:CD=3:2
.
Ответ. 13:23
.
Указание. Продолжите боковые стороны трапеции до пересечения в точке K
и воспользуйтесь равенством
\frac{S_{\triangle KDC}}{S_{\triangle KPQ}}=\frac{KD}{KP}\cdot\frac{KC}{KQ}.
Рассмотрите два случая.
Решение. Продолжим боковые стороны трапеции до пересечения в точке K
. Треугольник KDC
подобен треугольнику KAB
с коэффициентом \frac{CD}{AB}=\frac{2}{3}
, значит, \frac{KD}{KA}=\frac{2}{3}
. Положим KD=2x
, AK=3x
. Тогда AD=x
, а так как AP:PD=3:2
, то
PD=\frac{2}{5}AD=\frac{2}{5}x,~KP=KD+PD=2x+\frac{2}{5}x=\frac{12}{5}x.
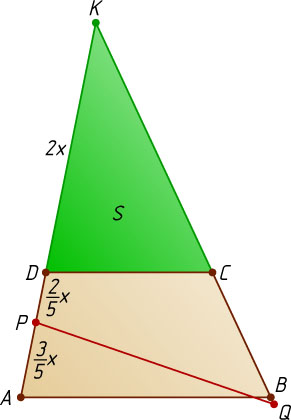
Предположим, что площадь четырёхугольника PDCQ
вдвое больше площади четырёхугольника APQB
(рис. 1). Обозначим S_{\triangle KDC}=S
. Тогда
S_{\triangle KAB}=\left(\frac{3}{2}\right)^{2}S_{\triangle KDC}=\frac{9}{4}S,~S_{ABCD}=\frac{9}{4}S-S=\frac{5}{4}S,
S_{PDCQ}=\frac{2}{3}S_{ABCD}=\frac{2}{3}\cdot\frac{5}{4}S=\frac{5}{6}S,~S_{\triangle KPQ}=S+\frac{5}{6}S=\frac{11}{6}S,~\frac{S_{\triangle KDC}}{S_{\triangle KPQ}}=\frac{S}{\frac{11}{6}S}=\frac{6}{11},
а так как
\frac{S_{\triangle KDC}}{S_{\triangle KPQ}}=\frac{KD}{KP}\cdot\frac{KC}{KQ}=\frac{2}{\frac{12}{5}}\cdot\frac{KC}{KQ}=\frac{5}{6}\cdot\frac{KC}{KQ}=\frac{6}{11}
(см. задачу 3007), то \frac{KC}{KQ}=\frac{36}{55}
. Тогда точка Q
лежит на продолжении стороны BC
за точку B
, так как \frac{KC}{KB}=\frac{2}{3}\gt\frac{36}{55}
.
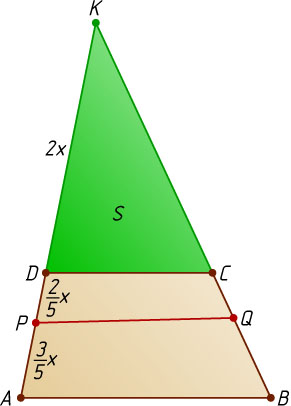
Пусть теперь площадь четырёхугольника PDCQ
вдвое меньше площади четырёхугольника APQB
(рис. 2). Тогда
S_{PDCQ}=\frac{1}{3}S_{ABCD}=\frac{1}{3}\cdot\frac{5}{4}S=\frac{5}{12}S,~S_{\triangle KPQ}=S+\frac{5}{12}S=\frac{17}{12}S,~\frac{S_{\triangle KDC}}{S_{\triangle KPQ}}=\frac{S}{\frac{17}{12}S}=\frac{12}{17},
а так как
\frac{S_{\triangle KDC}}{S_{\triangle KPQ}}=\frac{KD}{KP}\cdot\frac{KC}{KQ}=\frac{2}{\frac{12}{5}}\cdot\frac{KC}{KQ}=\frac{5}{6}\cdot\frac{KC}{KQ}=\frac{12}{17},
то \frac{KC}{KQ}=\frac{72}{85}
. Тогда точка Q
лежит на стороне BC
, так как \frac{KC}{KB}=\frac{2}{3}\lt\frac{72}{85}
, причём
\frac{CQ}{QB}=\frac{KQ-KC}{KB-KQ}=\frac{85-72}{108-85}=\frac{13}{23}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1995 (предварительный экзамен), № 4, вариант 2
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.30, с. 54

