2808. Вершины B
, C
, D
четырёхугольника ABCD
расположены на окружности с центром O
, которая пересекает сторону AB
в точке F
, а сторону AD
— в точке E
. Известно, что угол BAD
прямой, хорда EF
равна хорде FB
и хорды BC
, CD
, ED
равны между собой. Найдите угол ABO
.
Ответ. \frac{3\pi}{7}
.
Указание. Угол BAD
равен полуразности дуги BCD
и дуги EF
, не содержащей точку D
.
Решение. Точки C
и D
разбивают дугу BE
, не содержащую точку F
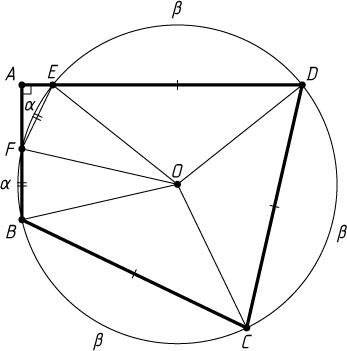
, на три равные дуги. Пусть \beta
— величина каждой из этих трёх дуг, а \alpha
— величина каждой из двух равных дуг BF
и EF
, не содержащих точку D
. Тогда
2\alpha+3\beta=2\pi,
а так как угол BAD
равен полуразности дуги BCD
и дуги EF
, не содержащей точку D
(см. задачу 27), то
\frac{2\beta-\alpha}{2}=\frac{\pi}{2}.
Из полученной системы уравнений находим, что \alpha=\frac{\pi}{7}
. Искомый угол ABO
находим из равнобедренного треугольника BOF
:
\angle ABO=\angle FBO=\frac{\pi}{2}-\frac{\alpha}{2}=\frac{\pi}{2}-\frac{\pi}{14}=\frac{3\pi}{7}.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1995, № 5, вариант 1
