2811. В четырёхугольнике ABCD
диагонали AC
и BD
относятся как 1:4
, а угол между ними равен 60^{\circ}
. Чему равен больший из отрезков, соединяющих середины противоположных сторон четырёхугольника ABCD
, если меньший равен \sqrt{26}
?
Ответ. \sqrt{42}
.
Указание. Середины сторон любого четырёхугольника являются вершинами параллелограмма, стороны которого параллельны диагоналям четырёхугольника и соответственно равны их половинам (см. задачу 1204).
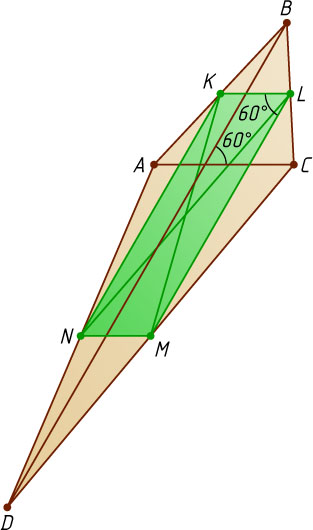
Решение. Пусть K
, L
, M
и N
— середины сторон соответственно AB
, BC
, CD
и AD
данного четырёхугольника ABCD
. Тогда KL
и MN
— средние линии треугольников ABC
и ADC
с общей стороной AC
, поэтому KL=MN
и KL\parallel MN
, значит, четырёхугольник KLMN
— параллелограмм. Его соседние стороны соответственно параллельны диагоналям данного четырёхугольника, значит, острый угол параллелограмма равен 60^{\circ}
. Кроме того, так как KL=\frac{1}{2}AC
и LM=\frac{1}{2}BD
, то \frac{KL}{LM}=\frac{AC}{BD}=\frac{1}{4}
.
Предположим, что KM\lt LN
. Тогда KM=\sqrt{26}
, а так как в параллелограмме меньшая диагональ лежит против меньшего угла, то \angle KLM=60^{\circ}
.
Положим KL=x
, LM=4x
. По теореме косинусов
KM^{2}=KL^{2}+LM^{2}-2KL\cdot LM\cos60^{\circ},
или 26=x^{2}+16x^{2}-4x^{2}
, откуда находим, что x^{2}=2
. Следовательно,
LN=\sqrt{KL^{2}+KN^{2}-2KL\cdot KN\cos120^{\circ}}=\sqrt{KL^{2}+LM^{2}+KL\cdot LM}=
=\sqrt{x^{2}+16x^{2}+4x^{2}}=\sqrt{21x^{2}}=\sqrt{21\cdot2}=\sqrt{42}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1995 (предварительный экзамен), № 6, вариант 2
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.16, с. 24
