2858. Точка, расположенная внутри правильного треугольника, удалена от его вершин на расстояния 5, 6 и 7. Найдите площадь треугольника.
Ответ. \frac{36\sqrt{6}+55\sqrt{3}}{4}
.
Указание. Отобразите точку M
симметрично относительно сторон данного треугольника.
Решение. Пусть M
— точка внутри правильного треугольника ABC
, причём AM=5
, BM=6
, CM=7
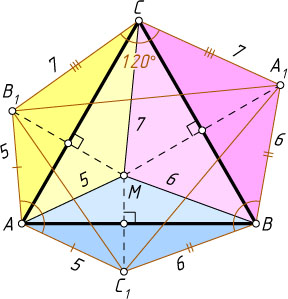
. Рассмотрим точки A_{1}
, B_{1}
и C_{1}
, симметричные точке M
относительно прямых BC
, AC
и AB
соответственно. В равнобедренных треугольниках AB_{1}C_{1}
, BA_{1}C_{1}
и CA_{1}B_{1}
известны боковые стороны и углы при вершинах A
, B
и C
, равные по 120^{\circ}
. Тогда площади этих треугольников равны соответственно \frac{25\sqrt{3}}{4}
, \frac{36\sqrt{3}}{4}
и \frac{49\sqrt{3}}{4}
. По теореме косинусов находим основания этих треугольников:
B_{1}C_{1}=5\sqrt{3},~A_{1}C_{1}=6\sqrt{3},~A_{1}B_{1}=7\sqrt{3}.
По формуле Герона находим, что площадь треугольника A_{1}B_{1}C_{1}
равна 18\sqrt{6}
. Тогда площадь шестиугольника AB_{1}CA_{1}BC_{1}
равна
\frac{25\sqrt{3}}{4}+\frac{36\sqrt{3}}{4}+\frac{49\sqrt{3}}{4}+18\sqrt{6}=\frac{110\sqrt{3}}{4}+18\sqrt{6}.
Поскольку треугольники AB_{1}C
, CA_{1}B
и AC_{1}B
соответственно равны треугольникам AMC
, CMB
и AMB
, то площадь шестиугольника AB_{1}CA_{1}BC_{1}
вдвое больше площади S
треугольника ABC
. Следовательно,
S_{\triangle ABC}=\frac{1}{2}\left(\frac{110\sqrt{3}}{4}+18\sqrt{6}\right)=\frac{55\sqrt{3}+36\sqrt{6}}{4}.
Примечание. 1. Если расстояния от точки внутри равностороннего треугольника до его вершин равны 3, 4 и 5, то его площадь равна \frac{25\sqrt{3}+36}{4}
.
2. См. также решение задачи 12373.
Источник: Журнал «Crux Mathematicorum». — 1975, № 7, задача 39, с. 64
Источник: Соросовская олимпиада. — 1995-1996, II, 2-й тур, 9 класс
