2870. Катеты прямоугольного треугольника равны 36 и 48. Найдите расстояние от центра вписанной в треугольник окружности до высоты, проведённой к гипотенузе.
Ответ. \frac{12}{5}
.
Указание. Вычислите указанную высоту, радиус вписанной окружности, расстояние от центра окружности до вершины прямого угла.
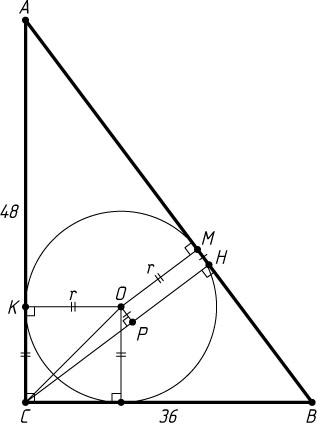
Решение. Первый способ. Пусть r
— радиус окружности с центром O
, вписанной в прямоугольный треугольник ABC
с катетами AC=48
и BC=36
, CH
— высота треугольника ABC
, M
и K
— точки касания окружности со сторонами AB
и AC
соответственно, P
— проекция центра O
на CH
. Тогда
AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{48^{2}+36^{2}}=\sqrt{12^{2}(4^{2}+3^{2})}=60,
OM=OK=r=\frac{AC+BC-AB}{2}=\frac{48+36-60}{2}=12
(см. задачу 217),
CH=AC\cdot\frac{BC}{AB}=48\cdot\frac{36}{60}=\frac{144}{5},
CP=CH-PH=CH-OM=CH-r=\frac{144}{5}-12=\frac{84}{5},
OC=\frac{OK}{\sin\angle OCK}=\frac{r}{\sin45^{\circ}}=r\sqrt{2}=12\sqrt{2},
Следовательно,
OP=\sqrt{OC^{2}-CP^{2}}=\sqrt{(12\sqrt{2})^{2}-\left(\frac{84}{5}\right)^{2}}=12\sqrt{2-\frac{49}{25}}=\frac{12}{5}.
Второй способ. Пусть r
— радиус окружности с центром O
, вписанной в прямоугольный треугольник ABC
с катетами AC=48
и BC=36
, CH
— высота треугольника ABC
, M
и K
— точки касания окружности со сторонами AB
и AC
соответственно, P
— проекция центра O
на CH
. Тогда
AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{48^{2}+36^{2}}=\sqrt{12^{2}(4^{2}+3^{2})}=60,
OM=OK=r=\frac{AC+BC-AB}{2}=\frac{48+36-60}{2}=12,
BH=\frac{BC^{2}}{AB}=\frac{36^{2}}{60}=\frac{108}{5},
BM=BK=BC-CK=BC-r=36-12=24,
OP=MH=BM-BH=24-\frac{108}{5}=\frac{12}{5}.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1996 (предварительный экзамен), № 6, вариант 1
