2874. В угол с вершиной A
, равный 60^{\circ}
, вписана окружность с центром O
. К этой окружности проведена касательная, пересекающая стороны угла в точках B
и C
. Отрезок BC
пересекается с отрезком AO
в точке M
. Найдите радиус окружности, вписанной в треугольник ABC
, если AM:MO=2:3
и BC=7
.
Ответ. \frac{7}{3\sqrt{3}}
.
Указание. Если данная окружность касается прямых BC
и AB
в точках P
и Q
соответственно, а AH
— высота треугольника ABC
, то \frac{AH}{OP}=\frac{AM}{OM}=\frac{2}{3}
, а полупериметр треугольника ABC
равен отрезку AQ
(см. задачу 4770).
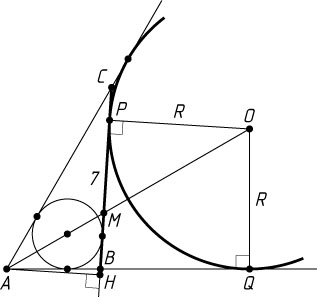
Решение. Пусть R
— радиус данной окружности, P
и Q
— её точки касания с прямыми BC
и AB
соответственно, AH
— высота треугольника ABC
, r
— радиус вписанной в треугольник ABC
окружности, p
— полупериметр треугольника ABC
. Тогда
p=AQ=OQ\ctg\angle OAQ=R\ctg30^{\circ}=R\sqrt{3}
(см. задачу 4805). Из подобия прямоугольных треугольников AHM
и OPM
следует, что \frac{AH}{OP}=\frac{AM}{MO}=\frac{2}{3}
, поэтому AH=\frac{2}{3}PO=\frac{2}{3}R
. Тогда
S_{\triangle ABC}=\frac{1}{2}BC\cdot AH=\frac{1}{2}\cdot7\cdot\frac{2}{3}R=\frac{7}{3}R.
С другой стороны,
S_{\triangle ABC}=pr=R\sqrt{3}\cdot r=Rr\sqrt{3}.
Из равенства \frac{7}{3}R=Rr\sqrt{3}
находим, что r=\frac{7}{3\sqrt{3}}
.
Источник: Вступительный экзамен на факультет психологии МГУ. — 1996, № 4, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.27, с. 62
